La formule de Leibniz

[doc123]

Bonsoir;
j'ai un petit problème dans l'application de la formule de Leibniz
on a pour tout x appartient à IR:



comment démontrer que


j'ai pensé à la récurrence mais non, donc enfin Leibniz
Aidez moi s.v.p

[Nightmare]

Salut,



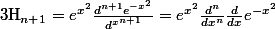Or, , d'ou le résultat en sortant le moins.

[doc123]

c'est par Leibniz ?

[Nightmare]

Ou vois-tu Leibniz ici?

Leibniz te permet de calculer une dérivée n-ème, ce n'est pas ce qu'on te demande ici ! (On ne te demande pas de calculer explicitement H(n))

[doc123]

merci; tant j'y suis comment je démontrer que :

j'ai une patite idée de reprendre la formule de

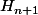
[Nightmare]

Oui, et c'est là qu'intervient Leibniz.

En effet, on a :


On voit qu'à partir de k=2, les termes de la somme sont nuls (puisque la dérivée seconde de est nulle). Termine le calcule.

[doc123]

Oui, mé en fait Leibniz s'applique à deux fonctions ?

[Nightmare]

Oui la formule de Leibniz permet d'exprimer la dérivée n-ème d'un produit en fonction des dérivées successives des facteurs. Remarque l'analogie avec le binome de Newton.

[doc123]

Je ne vois pas le rapport :
Remarque l'analogie avec le binome de Newton.avec Leibniz

je trouve ? est ce normal

[doc123]

ok, jé trouvé l'erreur;
mais par contre Je ne vois pas le rapport :
Remarque l'analogie avec le binome de Newton.avec Leibniz

[Nightmare]

n'oublie pas le coefficient binomial !!

Tu ne vois pas le rapport entre la formule de Leibniz et le binome de Newton? C'est fort quand meme...