Espérance mathématique

par **rifly01** » 10 Fév 2009, 21:33

Bonjour,

Est-ce que cette cette égalité est juste :

Noter la différence : Je somme sur deux ensembles différents

Merci d'avance,

par **Joker62** » 10 Fév 2009, 21:44

Haileau ;)

J'vois pas l'intérêt d'écrire ça sous forme de Somme...
Enfin sauf si tu t'es trompé et qu'à la place de R on trouve N dans la deuxième...

par **rifly01** » 10 Fév 2009, 21:47

Le premier membre me parait plus correcte.

Pour le deuxième. J'ai vu dans un livre [cf. Jean-Yves Ouvrard] que l'espérance est définie avec

.

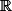
Ce sont des sommes. Car je suis dans le discret.

par **Joker62** » 10 Fév 2009, 21:52

Donc par définition

Et là on applique le théorème de transfert

Donc dans le cas discret, on a Omega(X) = N d'où l'apparition des sommes

par **rifly01** » 10 Fév 2009, 21:54

En utilisant la mesure de comptage

Merci!

Espérance mathématique

Espérance mathématique

Qui est en ligne