Fonction dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 19:04
par Ducobu » 07 Fév 2009, 19:04
Soit f la fonction définie sur R+ par f(x) = 
1) Montrer que, pour tout x strictement positif,
 sqrt{1+x} -1}{x}) =
= sqrt{1+x}+1})
2) Montrer que f est dérivable en x=1, et calculer f ' (1)Voilà l'exercice.
Pour ce qui est de calculer la dérivée, je sais le faire.
En revanche, pour l'égalité, je sèche.
Pouvez-vous me venir en aide ?
Merci bien.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 19:08
par Monsieur23 » 07 Fév 2009, 19:08
Aloha ;
Multiplie en haut et en bas par la quantité conjuguée
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 19:13
par Ducobu » 07 Fév 2009, 19:13
Quantité conjugué ?
Je suis en première.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 19:15
par Monsieur23 » 07 Fév 2009, 19:15
La quantité conjuguée de

est

.
Si tu veux faire passer une racine du dénominateur au numérateur ( et vice-versa ), tu multiplies en haut et en bas par la quantité conjuguée, ça marche à tous les coups :lol4:
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 19:18
par Ducobu » 07 Fév 2009, 19:18
Tu peux me faire un exemple avec des a,b,c ?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 19:21
par Monsieur23 » 07 Fév 2009, 19:21
Mettons que tu dois transformer

( aucun rapport avec ton exo, j'ai pris un truc au pif )
(\sqrt{a}+b)}{(\sqrt{a}-b)(\sqrt{a}+b)})
En développant :
(\sqrt{a}+b)}{a-b^2})
Et hop, plus de racine au dénominateur !
Tu comprends ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 19:48
par Ducobu » 07 Fév 2009, 19:48
(
 sqrt{1+x} -1)
) * (
sqrt{1+x}+1)
) = (

)*
)
(
^2 + 1+x+1)
) = (

)*
)
(

) = (

)*
)
(

) = (

)*
)
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 20:02
par Ducobu » 07 Fév 2009, 20:02
J'ai fait le calcul autrement, je me retrouve toujours avec un x en trop en facteur.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:08
par Monsieur23 » 07 Fév 2009, 20:08
Tu t'es trompé en développant.
 sqrt{1+x} -1}{x} = \frac{((1+x) sqrt{1+x} -1)((1+x) sqrt{1+x} +1)}{x((1+x) sqrt{1+x} +1)})
Développe en haut, tu auras ce que tu veux !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 20:16
par Ducobu » 07 Fév 2009, 20:16
il y a toujours un " x " en trop .
L'expression de droite, au dénominateur, le x au début en facteur. Il est en trop.
J'ai fait tout les calculs. Je ne comprends pas
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:18
par Monsieur23 » 07 Fév 2009, 20:18
Au numérateur, une fois développé, ça fait x³+3x²+3x.
En simplifiant par x, tu as bien ce que tu veux !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 20:30
par Ducobu » 07 Fév 2009, 20:30
quand je développe le numérateur je trouve :
x^3 + 2x² + x
POURQUOI?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:34
par Monsieur23 » 07 Fév 2009, 20:34
 sqrt{1+x} -1)((1+x) sqrt{1+x} +1) = ((1+x) sqrt{1+x})^2 - 1)
( identité remarquable ).
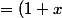^2 \times (1+x) - 1 = (1+x)^3 - 1)
(1+x)³ = x³+3x²+3x+1
C'est bon ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 21:04
par Ducobu » 07 Fév 2009, 21:04
Ouf! C'est bon, merci.
Aie, ce sont avec des erreurs de calculs comme celles-ci que je me plante en DS ...
Bon, Nous pouvons passer à la question 2) :id:
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 21:06
par Monsieur23 » 07 Fév 2009, 21:06
Yes !
Quelle est la définition de la dérivabilité en 1 ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 21:24
par Ducobu » 07 Fév 2009, 21:24
1 est la dérivée de x.
Je n'en sais pas plus :hein:
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 21:27
par Monsieur23 » 07 Fév 2009, 21:27
T'as pas un cours sur la dérivabilité ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 21:32
par Ducobu » 07 Fév 2009, 21:32
Apparemment non :triste:
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 21:38
par Monsieur23 » 07 Fév 2009, 21:38
f est dérivable en 1 si et seulement si (f(x) - f(1))/(x-1) admet une limite finie quand x tend vers 1 !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Ducobu
- Membre Relatif
- Messages: 287
- Enregistré le: 05 Mai 2005, 16:27
-
 par Ducobu » 07 Fév 2009, 21:40
par Ducobu » 07 Fév 2009, 21:40
Je ne connaissais pas cette définition.
Je peux l'appliquer directement ici ? sans démonstration ?
Ici f(1) = 1 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
