Somme et intégrale

par **sanssecondmembre** » 05 Fév 2009, 16:05

Bonjour,

Je voudrais établir: intégrale de 0 à 1 de: e^x ln x dx = - somme de 1/nn! sur n de 1 à l'infini.

J'ai intégré par parties mais ça ne donne rien. Je pense donc que le cheminement se fera par la série de 1/nn!, mais je ne sais que faire. Je ne suis pas parvenu à l'encadrer non plus. Quelqu'un pourait-il me donner une ou plusieurs pistes? Merci d'avance :hein:

par **Joker62** » 05 Fév 2009, 16:14

Le lnx il est dans l'exponentielle ou pas ?

par **sanssecondmembre** » 05 Fév 2009, 16:20

non, c'est l'intégrale de la fonction exp*ln sur ]0;1]

par **fatal_error** » 05 Fév 2009, 16:31

salut,

je prends le risque de dire une connerie, mais l'intégrale est la pas divergente en 0?
parce que la serie elle, elle converge bien...

par **phryte** » 05 Fév 2009, 17:13

Bonsoir.

0 à 1 de: e^x ln x dx

cela fait -0.25

- somme de 1/(n*n!) de 1 à l'infini.

cela fait -1.317902...

par **yos** » 05 Fév 2009, 17:26

Calcule la somme de la série des

.
Une IPP pour l'intégrale.

par **fatal_error** » 05 Fév 2009, 17:44

du coup ca me pertube...
En faisant une IPP j'ai

en mettant la seconde en serie :

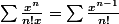
c'est CVU donc j'intervertis somme et intégrale :

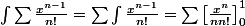
donc

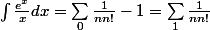
car

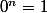
Mais il reste quand même le premier terme entre crochets.

???

J'arrive pas a trouver la boulette...anyhelp? :cry:

par **yos** » 05 Fév 2009, 17:47

fatal_error a écrit:En faisant une IPP j'ai

Elle est là :
Dans le second membre c'est divergent -divergent.

par **fatal_error** » 05 Fév 2009, 17:48

merci, je vais ravitailler la pense avant d'y regarder plus attentivement :-)

par **sanssecondmembre** » 05 Fév 2009, 18:41

merci pour la piste, je vais me débrouiller à partir de là. Je n'avait pas penser à transformer le second membre en série entière et d'intervertir somme intégrale. Je vous remercie pour l'aide. Toutefois si vous avez encore envi d'en discuter entre vous, je vous en prie, amusez-vous!

Somme et intégrale

somme et intégrale

Qui est en ligne