Primitive avec LN

par **Parizio** » 02 Fév 2009, 16:55

Bonjour tout le monde !

Les données sont : F(x) = xLN(x² + 4x +3) + 3LN(x + 3) + LN(x+1) - 2x

a) Je dois Montrer que F est une primitive de f (sachant que f(x) = LN(x² + 4x + 3).
b) Calculer l'air de A du domaine du plan limité par la courbe C, l'axe des abscisses et les droites d'équations x = 0 et x = 3 (A = Integrale de 0 a 3 f(x) dx = F(3) - F(0) unités d'aire).

Donner la valeur exacte puis une valeur approchée a 10^-2 prés.

Auriez vous une idée ?
Merci.

par **phryte** » 02 Fév 2009, 17:17

Bonsoir.
Une primitive de ln(x) est : x ln(x) - x
.....

par **Parizio** » 02 Fév 2009, 17:19

aah, je l'utilise en partant de F ou de petit f ?
Je comprends pas trop

par **Kah** » 02 Fév 2009, 17:32

tu peux aussi (plus abordable) deriver F, et comme dans les films de cow-boy, tu tombera pile sur f.

par **Parizio** » 02 Fév 2009, 17:34

Kah a écrit:tu peux aussi (plus abordable) deriver F, et comme dans les films de cow-boy, tu tombera pile sur f.

Ah oui, en dérivant F je trouve f. Est ce que je peux rassembler les LN ? en mettant tout sous un même LN et je multiplie les termes ?

par **Parizio** » 02 Fév 2009, 20:20

Mais pour la seconde question, comment dois-je procédé ?? je l'ai vraiment pas comprise avec l'histoire de l'aire ...

par **phryte** » 02 Fév 2009, 21:54

je l'ai vraiment pas comprise avec l'histoire de l'aire ...

Fais un schéma et utilise la primitive.

par **Parizio** » 03 Fév 2009, 17:26

Excusez moi, a propos de la primitive, j'ai pas compris comment la dériver.
Je la dérive depuis l'expression meme ou je la simplifie ?
Je pense la simplifier (multiplier les deux derniers LN entre eux ce qui me donne la même terme que le premier LN ac 3 devant.
Je sais pas apès comment faire..?

Merci.

par **Parizio** » 03 Fév 2009, 18:21

Personne pourrait m'éclairer ?

par **phryte** » 04 Fév 2009, 08:25

Bonjour.

j'ai pas compris comment la dériver. Je la dérive depuis l'expression meme ou je la simplifie ?

Pour a)
Par exemple sachant que ln(u)' = u'/u:
Dérivée de : xLN(x² + 4x +3) --> LN(x² + 4x +3) + 2x^3/(x² + 4x +3)

Il faut aussi remarquer que : x² + 4x +3 = (x+3)(x+1)
....
Pour le b) il suffit de faire ce qui est indiqué F(3) - F(0)
...

par **mathelot** » 04 Fév 2009, 09:31

Bj,

une primitive de

est

sur

cette remarque permet de trouver une primitive de

et de

on dira qu'on intégre une fonction composée :zen:

d'où une primitive de

ensuite, on peut compliquer tout ça en
une primitive de

est

sur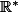

car, malheureusement , le trinome

est strictement positif si

et

et on primitive sur la réunion

domaine qui n'est pas un intervalle.

Primitive avec LN

Primitive avec LN

Qui est en ligne