Ordre d'un élément de (Z/2^nZ)*
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Fév 2009, 19:09
par yos » 01 Fév 2009, 19:09
Bonsoir.
Sauriez-vous trouver l'ordre de 5 dans le groupe
^\times)
?
J'ai une méthode que je trouve compliquée.
-
netpro-sniper69
- Membre Naturel
- Messages: 21
- Enregistré le: 02 Fév 2008, 14:54
-
 par netpro-sniper69 » 01 Fév 2009, 19:34
par netpro-sniper69 » 01 Fév 2009, 19:34
bonjour
je me trompe peut etre mais si tu ecrit q = ordre de 5 alors
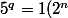)
ca doit pouvoir marcher comme ca nn ?
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 01 Fév 2009, 19:42
par skilveg » 01 Fév 2009, 19:42
Si je ne me plante pas, la technique classique consiste à vérifier par récurrence que
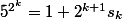
où
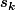
est un entier impair; après c'est presque fini. (Du coup on trouve un ordre qui vaut
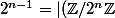^{\!\times}|)
, ce qui prouve que
^{\!\times})
est cyclique.)
[C'est évidemment faux, c'est plutôt
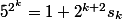
. Voir la suite du fil pour le reste.]
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Fév 2009, 20:22
par yos » 01 Fév 2009, 20:22
Non l'ordre est
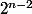
et
^X)
est pas cyclique.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 01 Fév 2009, 20:54
par leon1789 » 01 Fév 2009, 20:54
yos a écrit:Bonsoir.
Sauriez-vous trouver l'ordre de 5 dans le groupe
^\times)
?
J'ai une méthode que je trouve compliquée.
Si tu as envie de parcourir rapidement
http://maths-forum.com/showthread.php?t=67239&page=1&pp=10c'est la méthode habituelle...
EDIT : je viens de parcourir cette discussion... bon, c'est pas la joie...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Fév 2009, 21:14
par yos » 01 Fév 2009, 21:14
Merci : ma méthode est donc pas pire.
Curieux que tu te souviennes de ce fil.
Thsq : faut absolument que tu vois ce fil, d'autres que nous avaient déjà bizuté Léon on dirait

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Fév 2009, 14:31
par leon1789 » 02 Fév 2009, 14:31
yos a écrit:Merci : ma méthode est donc pas pire.
Curieux que tu te souviennes de ce fil.
Tu parles que je m'en souviens ! Une personne qui veut faire cet exo , dans les plus brefs délais, mais sans savoir ce qu'est l'ordre d'un élément, ni même connaitre Z/nZ , ça laisse des traces :we:
yos a écrit:Thsq : faut absolument que tu vois ce fil, d'autres que nous avaient déjà bizuté Léon on dirait
Tu vois pourquoi je m'en souviens de ce fil ! :id:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Fév 2009, 18:57
par ThSQ » 02 Fév 2009, 18:57
yos a écrit:faut absolument que tu vois ce fil, d'autres que nous avaient déjà bizuté Léon on dirait
yos :
chuttt, il va finir par avoir des soupçons 
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 02 Fév 2009, 19:11
par ffpower » 02 Fév 2009, 19:11
:ptdr: ,me suis bien marré
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 02 Fév 2009, 19:37
par Joker62 » 02 Fév 2009, 19:37
Purée la patiente !
J'aurais déjà cherché son adresse sur le net pour régler mes envies de meurtres lol
Chapeau Chapeau Léon ;)
Et classe en plus la soluce :)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Fév 2009, 19:43
par yos » 02 Fév 2009, 19:43
Un véritable sketch ce fil. Dans la chaleur du moi d'aout, Léon devait s'ennuyer.
Et c'est quoi l'ordre de 2 dans
^\times)
?
J'ai l'impression qu'il engendre mais je suis pas sûr.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Fév 2009, 20:34
par leon1789 » 02 Fév 2009, 20:34
Joker62 a écrit:Purée la patiente !
J'aurais déjà cherché son adresse sur le net pour régler mes envies de meurtres lol
Chapeau Chapeau Léon

Et classe en plus la soluce

Merci. C'est quand même un peu trop calculatoire.
yos a écrit:Un véritable sketch ce fil. Dans la chaleur du moi d'aout, Léon devait s'ennuyer.
Oui, visiblement, j'avais vraiment rien à faire ... :zen:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Fév 2009, 20:38
par leon1789 » 02 Fév 2009, 20:38
yos a écrit:Et c'est quoi l'ordre de 2 dans
^\times)
?
J'ai l'impression qu'il engendre mais je suis pas sûr.
On peut peut-être prouver
 = k+1)
? par récurrence ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Fév 2009, 20:57
par leon1789 » 02 Fév 2009, 20:57
yos a écrit:Et c'est quoi l'ordre de 2 dans
^\times)
?
J'ai l'impression qu'il engendre mais je suis pas sûr.
On peut prouver
 = k+1)
par récurrence.
Ton résultat en découle : 2 est effectivement d'ordre

dans
^\times)
, donc générateur.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Fév 2009, 23:03
par yos » 02 Fév 2009, 23:03
En effet ça marche. Merci. Voilà donc une famille cyclique infinie.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 03 Fév 2009, 00:17
par skilveg » 03 Fév 2009, 00:17
yos a écrit:Non l'ordre est
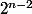
et
^X)
est pas cyclique.
Oui, je suis désolé de ne pas avoir corrigé plus tôt, je me suis rendu compte de mon erreur un peu tard.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
?