Petit problème de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:12
par Ptiboudelard » 31 Jan 2009, 19:12
Bonsoir !
J'ai un petit souci dans un calcul de limite :
Soit
=\frac{x}{e^{x}-1})
J'ai trouvé que la limite en 0 etait 1, mais en +oo je n'y arrive pas !
Auriez vous une piste pour moi ?
Merci !
-
SimonB
 par SimonB » 31 Jan 2009, 19:29
par SimonB » 31 Jan 2009, 19:29
Tu n'as jamais vu que l'exponentielle l'emportait sur tous les polynômes ?
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:35
par Ptiboudelard » 31 Jan 2009, 19:35
Euh, eh bien, je savais que lim xe^x en +oo est égale à +oo car l'exponentielle l'emporte, mais je ne savais pas que c'était valable pour tout polynome.
Mais je ne vois pas comment appliquer cette limite ?
-
PsY
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Juil 2008, 18:53
-
 par PsY » 31 Jan 2009, 19:40
par PsY » 31 Jan 2009, 19:40
Pas exactement simonB, l'exponentielle est négligeable devant le x factorielle qui lui est negligeable devant la fonction x puissance x
e^x << x! << x^x en l'infini
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:41
par Ptiboudelard » 31 Jan 2009, 19:41
ben c'est ce que moi javais appris. Mais du coup, comment faire pour cette limite ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 31 Jan 2009, 19:44
par ThSQ » 31 Jan 2009, 19:44
DL, L'Hopistal, ...
-
PsY
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Juil 2008, 18:53
-
 par PsY » 31 Jan 2009, 19:45
par PsY » 31 Jan 2009, 19:45
Fais passer le x en dessous du e^x - 1
ca va te donner 0 je pense
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:46
par Ptiboudelard » 31 Jan 2009, 19:46
oula ... je ne connais pas le theoreme de l'hospital ... mais n'y a t il pas une equivalence ? ou quelquechose comme ca ? ( que signifie DL?)
-
PsY
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Juil 2008, 18:53
-
 par PsY » 31 Jan 2009, 19:48
par PsY » 31 Jan 2009, 19:48
developpement limité
mais fais comme je t'ai dit et tu verras c'est reglé
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 31 Jan 2009, 19:49
par ThSQ » 31 Jan 2009, 19:49
DL = Développement limité
Ceci dit le plus simple ici :
(x-0)/(e^x- e^0) -> dérivée en 0 et e^-x.
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:51
par Ptiboudelard » 31 Jan 2009, 19:51

donc après ca nous donne 0 ?
-
SimonB
 par SimonB » 31 Jan 2009, 19:55
par SimonB » 31 Jan 2009, 19:55
PsY a écrit:Pas exactement simonB, l'exponentielle est négligeable devant le x factorielle qui lui est negligeable devant la fonction x puissance x
Tu m'expliques comment tu définis x! pour x non entier ? ...
Pour Ptiboudelard : ce que veut dire ThSQ, c'est que tu peux écrire que ton expression est égale à

, et que tu peux reconnaître dans le terme du dessous un nombre dérivé.
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 19:56
par Ptiboudelard » 31 Jan 2009, 19:56
oui mais avec la maniere que j'ai proposée plus haut, ca marche ! non ?
-
PsY
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Juil 2008, 18:53
-
 par PsY » 31 Jan 2009, 20:04
par PsY » 31 Jan 2009, 20:04
Ptiboudelard a écrit:
donc après ca nous donne 0 ?
tu attends quoi pour découper en deux ce qu'il y a au dénominateur
-
SimonB
 par SimonB » 31 Jan 2009, 20:07
par SimonB » 31 Jan 2009, 20:07
Ptiboudelard a écrit:oui mais avec la maniere que j'ai proposée plus haut, ca marche ! non ?
Je n'ai pas compris ce que tu disais. Ton égalité est juste, et après ?
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 20:12
par Ptiboudelard » 31 Jan 2009, 20:12
lim e^x/x = +oo
lim 1/x = 0
donc lim [1/((e^x/x)-(1/x))] = 0
-
SimonB
 par SimonB » 31 Jan 2009, 20:17
par SimonB » 31 Jan 2009, 20:17
Oui. Mais si tu savais déjà que
=+\infty)
, c'était pas la peine de faire tout ça ! Il suffit de remarquer que

se comporte comme
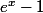
en l'infini, donc que la limite de

était la même que celle de
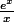
...
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 20:18
par Ptiboudelard » 31 Jan 2009, 20:18
en fait c'était là que résidait mon probleme. Je pensais que je ne pouvais pas affirmer que lim x/e^x et e^x/x était pareilles ...
-
SimonB
 par SimonB » 31 Jan 2009, 20:32
par SimonB » 31 Jan 2009, 20:32
Sont l'inverse l'une de l'autre plutôt !
-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 31 Jan 2009, 20:36
par Ptiboudelard » 31 Jan 2009, 20:36
[...]donc que la limite de
 était la même
était la même que celle de
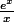
...
?? oula ... j'ai du mal à saisir ... :-S
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités