Base d'un orthogonal

[dim20]

Bonjour,
Je ne sais pas comment répondre à la question : donner une base de H et de l'orthogonal de H :

E=R², f(x,y)=x1*y1 -x2*y2 , H={x, x1=x2}

Comment faut-il répondre à ce genre des questions? Que faut-il chercher?

Merci beaucoup pour votre aide!

[laki]

bonjour

la condition x1=x2 pour les vecteurs appartenant à H te montre que
H=vect(e) où e=(1;1) ! je te laisse en faire la preuve ... H est donc de dimension 1. Tu en deduis aussi que l'orthogonal est de dimension 1, donc de la forme vect(f) où f est un vecteur orthogonal à e.
Il te suffit de trouver un vecteur non nul orthogonal à e pour le produit scalaire canonique.

a la prochaine

[skilveg]

Justement, d'après ce que j'ai compris, le produit scalaire n'est pas le produit scalaire usuel.

Dans ce cas il faut faire attention: comme la forme est non dégénérée, la somme des dimensions de l'hyperplan et de son orthogonal est bien 2, mais on n'a pas 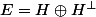(car est isotrope i.e. la restriction à de la forme est dégénérée).