DM de Noël

[Legarsympa]

Bonjour, je suis un élève de 1èreS et d'habitude je m'en sors dans mes dm mais là je suis complètement perdu et je ne comprends pas (ma prof a avoué s'etre défoulé en le faisant), en effet sur la dizaine d'exercices 2 me posent problème :

Exercice 1 :

Le plan est rapporté à un repère orthonormé (O;i;j)
Soit C le cercle de centre I(-1;2) passant par O

1) Montrer que M (x;y) appartient à C si et seulement si x²+y²+2x-4y=0
2) m est un nombre et Dm est la droite d'équation y=mx+9
a) tracer C, D0, D1, D2, D-5,5 et D5
b) Emettre une conjecture concernant le nombre de points d'intersection de Dm avec C, m variant dans R
3) Démontrer cette conjecture par le calcul

J'ai réussi à faire le 1) et le 2) mais je ne sais pas comment démmontrer ma conjecture par un calcul

Exercice 2 :

On coupe un fil de fer de longueur 48 mètres en deux parties. L'une permet de construire un carré, l'autre un triangle équilatéral.
Comment doit-on couper ce fil pour que la somme des deux aires du carré et du trianagle soit minimale ?

Je dirai que je n'ai pas réussi celui-là car mes résultats sont tout simplement aberrants !


En espérant une réponse
Merci d'avance

[XENSECP]

C'est quoi ta conjecture déjà ^^

[Zweig]

Salut,

Exercice 2 :

Soient et les longueurs des deux parties. On a .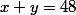
L'aire du carré est et l'aire du triangle équilatéral est .

On doit donc trouver le minimum de . C'est une fonction à deux variables. A priori, on ne sait pas faire. Sauf que l'on a 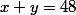, donc on peut se ramener à l'étude d'une fonction du second degré à une seule variable. Et là, tu sais faire.

[oscar]

Bonjour
EX 2
Soit c1 le côté du carré et c2 le côté du trianhgle équilatéral= 48-c1
Aire carré = c1²= S
Aire tr. équilatéral S' = 1/4 ( 48-c1)² V3
Calcule f(c1) = S+S'

[Sve@r]

On coupe un fil de fer de longueur 48 mètres en deux parties. L'une permet de construire un carré, l'autre un triangle équilatéral.
Comment doit-on couper ce fil pour que la somme des deux aires du carré et du trianagle soit minimale ?

Bonjour
EX 2
Soit c1 le côté du carré et c2 le côté du trianhgle équilatéral= 48-c1
Aire carré = c1²= S
Aire tr. équilatéral S' = 1/4 ( 48-c1)² V3
Calcule f(c1) = S+S'

Et étudie les limites de f pour avoir l'aire minimale (calcul de la dérivée, sens de variation, etc)

[Zweig]

Il y en a pas besoin. On obtient une fonction du second degré f(x) = ax² + bx + c et on sait que le minimum est atteint en x = -b/2a

[Legarsympa]

Merci d'avoir tant répondu pour l'esercice 2, mes conjectures pour l'exercice 1 sont les suivantes :
- deux points d'intersection pour m appartenant à ] moins l'infini ; -5,5[ ou à
]2 ; plus l'infini[
- un point d'intersection pour m=-5,5 et m=2
- pas de point d'intersection pour m appartenant à ]-5,5 ; 2[

[titicaca62]

Bonjour,
Voilà j'ai le même même exercice c'est à dire celui du fil...
Vos conseils m'ont bien aidés mais je bloque sur quelque chose qui est particulièrement simple.

Voilà,
j'ai posé donc les inconnus ...
J'ai dit que y= 48 - x pour pouvoir n'avoir qu'un seul inconnu dans la fonction de la somme des aires...
Ce qui me donne après avoir tout mis sur le même dénominateur ceci :

((4+racine de 3)x²)/4 - 24 racine de 3 (x) + 576 racine de trois

Or lorsque je calcule le discriminant celui-ci est négatif ..
Je ne vois pas du tout où est mon erreur, ca serait gantil un petit peu d'aide svp ...

Merci d'avance.
Matt.