Titre non conforme
Réponses à toutes vos questions du CP à la 3ème
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 14:00
par of.ey » 29 Jan 2009, 14:00
Bonjour tout le monde j'ai un dm mais je n'arrive vraiment pas
Voici l'enoncé:
determiner les entiers relatifs p et q tels que
2 puissance p x 5 puissance q = 1 :125 000
autre enoncé:
demontrer que a² + ab +b² = (a+b/2)² + 3b²/4
en deduire que a² +ab +b² est positif
Merci d'avance
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 14:18
par yvelines78 » 29 Jan 2009, 14:18
bonjour,
2 puissance p x 5 puissance q = 1 :125 000
2^p*5^q=

125000=125*10^3=5^3*(2*5)^3=5^3*2^3*5^3
fais maintenant un produit en croix et réfléchis a^0=?
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 14:22
par yvelines78 » 29 Jan 2009, 14:22
demontrer que a² + ab +b² = (a+
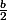
)² + 3

)
développe
(a+
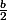
)² + 3

et retrouve a² + ab +b²
considérons l'expression (a+
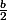
)² + 3

un carré est toujours positif
la somme de 2 carrés est ......
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 14:32
par of.ey » 29 Jan 2009, 14:32
je suis en train de reflechir , pourrais-tu me dire si mon raisonnement est juste ?
2^p*5^q = 1: 5^3*2^3*5^3
2^p*5^q*5^3*2^3*5^3:1
2^p*2^3*5^q*5^3*5^3:1
2^(p+3)*5^(q+3+3):1
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 14:34
par of.ey » 29 Jan 2009, 14:34
yvelines78 a écrit:développe
(a+
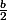
)² + 3

et retrouve a² + ab +b²
considérons l'expression (a+
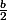
)² + 3

un carré est toujours positif
la somme de 2 carrés est ......
l'espression est (a+b/2)² + 3b²/4
la somme de deux carrés est donc toujours positives mais pour le prouver il fauit que je le developpe?
est ce qu'il faut que j'utilise une identite remarquable?
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 14:36
par yvelines78 » 29 Jan 2009, 14:36
of.ey a écrit:je suis en train de reflechir , pourrais-tu me dire si mon raisonnement est juste ?
2^p*5^q = 1: 5^3*2^3*5^3
2^p*5^q*5^3*2^3*5^3:1
2^p*2^3*5^q*5^3*5^3:1
2^(p+3)*5^(q+3+3)=1
2^0=?????,
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 14:37
par yvelines78 » 29 Jan 2009, 14:37
of.ey a écrit:la somme de deux carrés est donc toujours positives mais pour le prouver il fauit que je le developpe?
est ce qu'il faut que j'utilise une identite remarquable?
bien sûr!!!!!
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 14:42
par of.ey » 29 Jan 2009, 14:42
yvelines78 a écrit:2^0=?????,
2^0 fait 0
2^p+3 * 5^q+6 =1?
Mais après je ne vois pas comment faire
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 14:51
par of.ey » 29 Jan 2009, 14:51
yvelines78 a écrit:bien sûr!!!!!
(a+b/2)² + 3b²/4
= a²+2*a*b/2 + b/2²+ 3b²/4
= a² + 2a/1 *b/2 +b/2² + 3b²/4
= a² + 2ab/2 + b²/1 + 3b²/4
= a² + 2ab/2 +2b²/4 + 3b²/4
= a² + 2ab/2 + 5b²/4
est- ce que j'ai le droit si c'est juste , de barré pour le 2ab/2 le 2 d'en haut et celui d'en bas?
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 15:02
par yvelines78 » 29 Jan 2009, 15:02
of.ey a écrit:2^0 fait 0
2^p+3 * 5^q+6 =1?
Mais après je ne vois pas comment faire
c'est faux
2^0=1, va voir ton cours sur les racines!!!
10^0=1 l'exposant 0 marque qu'il n'y a pas de zéro derrière le 1
10^1=10 l'exposant 1 marque qu'il y a un 0 derrière le 1
10²=100 l'exposant 2 marque qu'il y a deux 0 derrière le 1
etc.....
cela aide pour la suite
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:10
par of.ey » 29 Jan 2009, 15:10
yvelines78 a écrit:c'est faux
2^0=1, va voir ton cours sur les racines!!!
10^0=1 l'exposant 0 marque qu'il n'y a pas de zéro derrière le 1
10^1=10 l'exposant 1 marque qu'il y a un 0 derrière le 1
10²=100 l'exposant 2 marque qu'il y a deux 0 derrière le 1
etc.....
cela aide pour la suite
desoler :s
je crois avoir compris seulement il faudrait que 5^0 fasse 1 mais je n'en suis pas sure
si c'est juste cela voudrait dire que:
2^p+3 * 5 ^q+6
p= -3
q=-6
car 2^-3+3 * 5 ^-6+6 =1 ?
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 15:12
par yvelines78 » 29 Jan 2009, 15:12
of.ey a écrit:desoler :s
je crois avoir compris seulement il faudrait que 5^0 fasse 1 mais je n'en suis pas sure
si c'est juste cela voudrait dire que:
2^p+3 * 5 ^q+6
p= -3
q=-6
car 2^-3+3 * 5 ^-6+6 =1 ?
c'est exact
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 15:13
par yvelines78 » 29 Jan 2009, 15:13
of.ey a écrit:(a+b/2)² + 3b²/4
= a²+2*a*b/2 +( b/2)²+ 3b²/4
= a² + 2a/1 *b/2 +b²/4 + 3b²/4
= a² + 2ab/2 + 4b²/4
= a² + 2ab/2 +b²
= a² + ab + b²
est- ce que j'ai le droit si c'est juste , de barré pour le 2ab/2 le 2 d'en haut et celui d'en bas?
oui

=ab
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:14
par of.ey » 29 Jan 2009, 15:14
yvelines78 a écrit:c'est exact
merccii beaucoup pour ton aide :we: :we: :we:
pourrais tu juste me dire si mon raisonnement pour l'autre enoncé était juste?
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:15
par of.ey » 29 Jan 2009, 15:15
[quote="of.ey"]merccii beaucoup pour ton aide :we: :we: :we:
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:16
par of.ey » 29 Jan 2009, 15:16
encore merci !!!!!
j'ai enfin compris :we:
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 29 Jan 2009, 15:17
par yvelines78 » 29 Jan 2009, 15:17
of.ey a écrit: of.ey a écrit:merccii beaucoup pour ton aide :we: :we: :we:
j'ai fait des corrections dans le post c'est exact
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:18
par of.ey » 29 Jan 2009, 15:18
je vien s de voir encore merci :)
-
of.ey
- Membre Naturel
- Messages: 25
- Enregistré le: 28 Jan 2009, 13:56
-
 par of.ey » 29 Jan 2009, 15:30
par of.ey » 29 Jan 2009, 15:30
une derniere question
après avoir trouver que a² + ab + b²= (a+b/2)² + 3b²/4 on me demande d'en deduire que a² + ab +b² est positifs comment je peux faire
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Jan 2009, 00:00
par yvelines78 » 30 Jan 2009, 00:00
of.ey a écrit:l'espression est (a+b/2)² + 3b²/4
la somme de deux carrés est donc toujours positives mais pour le prouver il fauit que je le developpe?
est ce qu'il faut que j'utilise une identite remarquable?
non un carré est positif (a+b/2)²>0
b²/4>0 et donc 3b²/4>0
la somme de 2 nombres >0 est >0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
)² + 3

)² + 3

