Application numerique KKT
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 28 Jan 2009, 16:30
Bonjour, j'ai une application numerique en optimisation avec contraintes que je ne sait pas faire. Voila le systeme :
min
)
sous contraintes
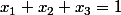
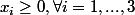
Voila donc ce que j'ai fait mais il me semble qu'il me manque des egalités.
Si je pose
=\frac{1}{2}(x_1^2+x_2^2+x_3^2))
et
=x_1+x_2+x_3-1)
Si je fait KKT, à partir de la tous les x sont des x barre.
J'obtiens donc
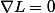
donc
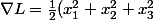 +\beta \nabla h(x_1,x_2,x_3)=(0,0,0))
et
=0)
donc
 +\beta(1,1,1)=(0,0,0))
et
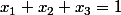
Apres avoir fait les calculs j'obtient :
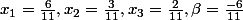
Alors il se trouve que ca tombe bien mes xi sont tous superieurs a 0 mais je ne l'ai pas reellemnt pris en compte.
Pourriez vous m'aider.
Merci d'avance
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 28 Jan 2009, 18:24
Bj
Vu la symétrie en x1,x2,x3 tes résultats me paraissent bizarres
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 28 Jan 2009, 18:53
En fait il se trouve que j'ai fait une erreur dans l'enoncé voila le corrigé:
min
)
sous contraintes
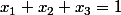
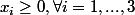
Je corrige donc ce que j'ai fait:
Je pose
=\frac{1}{2}(x_1^2+2x_2^2+3x_3^2))
et
Si je fait KKT, à partir de la tous les x sont des x barre.
J'obtiens donc
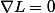
donc
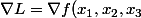 +\beta \nabla h(x_1,x_2,x_3)=(0,0,0))
et
donc
et
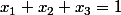
Apres avoir fait les calculs, donc j'ai ces resultats la :
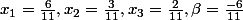
Merci pour votre réponse.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 28 Jan 2009, 20:15
Ok mais est-ce bien un minimum?
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 28 Jan 2009, 20:43
Justement je pense que c'est la le probleme, pourriez vous m'indiquer ce que je dois faire pour résoudre ce soucis?
Merci pour votre reponse
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 29 Jan 2009, 09:17
jeremy58 a écrit:Justement je pense que c'est la le probleme, pourriez vous m'indiquer ce que je dois faire pour résoudre ce soucis?
Merci pour votre reponse
g(x1,x2) = f(x1,x2,1-x1-x2)
tu développes g( (6/11) + h , (3/11) + k) ( par Taylor ou à la main)
tu montres que ; g( (6/11) + h , (3/11) + k) = g(6/11, 3/11) + quantité positive
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
