Bonsoir tout le monde et merci d'avance pour l'aide que vous devriez m'apporte.
Voilà un peu plus de 1 semaine que l'on a commencé les logarithme népérien, et je ne comprends absolument rien !
J'ai beau relire les formules et tenter de faire les exercices rien n'y fait !
Depuis 3 cours, le prof nous a donné un gros exercice type BAC et je vois que tout la classe et moi même sommes totalement dans la semoule...
Nous avons fait pas mal de chopses sur cet exercice mais voila ce qui est important.
f(x)=x+ 1/2 + ln x/x définie sur l'intervalle I ]0;+l'infini[
Démontrer que F(x): (x²+x+ (ln x)²)/2
Montrer que F est une primitive de f sur l'intervalle ]0;+l'infini[
Il y a d'autres questions mais je vais essayer de me débrouiller tout seul...
Mais pour celle je ne comprends pas... tout ce que j'ai fait sur les primitives ce présenté sous la forme f(x)= u/v sur un I donné d'où F(x): ... ln (v)
Je sais pas si je m'exprime trés bien mais cela donné par exemple f(x)=3/(x-1) sur I:]1;+l'infini[ d'ou F(x): 3 ln (x-1)
Voilà merci d'avance... je vous préviens je ne suis pas un cador en maths...
Neper... 1ére ES
6 messages
- Page 1 sur 1
Pour montrer que F(x) est une primitive de f(x) , il suffit de montrer que f(x) est la dérivée de F(x)
à savoir que :
(ln x )² = u² dont la dérivée est 2 u u'
1ère ES , avec primitives et logarithmes ?
qui a parlé d'allègement des programmes ?
Vous allez vous reposer en cours de maths l'année prochaine ?
à savoir que :
(ln x )² = u² dont la dérivée est 2 u u'
1ère ES , avec primitives et logarithmes ?
qui a parlé d'allègement des programmes ?
Vous allez vous reposer en cours de maths l'année prochaine ?
Merci de ta réponse, mais je en comprends pas, tu dis que (ln x)²=u² , mais u² ici ce serait donc égal a 1² non??
et si je cherche la dérivée avec la formule que tu m'as donné, 2u u'
Sa me donne 2 x1 x1 donc 2 et je vais avoir du mal à retomber sur f(x) avec ce 2...
je suis complétement perdu :triste:
et si je cherche la dérivée avec la formule que tu m'as donné, 2u u'
Sa me donne 2 x1 x1 donc 2 et je vais avoir du mal à retomber sur f(x) avec ce 2...
je suis complétement perdu :triste:
logarithme en 1ère S=dûr
Bonjour,
voilà quelques indications:
la fonction exponentielle est continue,strictement croissante,jamais nulle,
dérivable de
avec y'=y , y(0)=1, y(a+b)=y(a)y(b).
une relation s'inverse, tout en restant identique à elle-même:
si Pauline est la femme de Jean,Jean est le mari de Pauline.
De même, si x est réel et y>0,
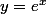 est la même chose que (équivaut à)
est la même chose que (équivaut à) 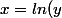)
ainsi, chaque fois que tu connais une propriété de l'exponentielle,
tu en déduis une propriété du logarithme népérien:
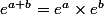
si et
et 
on inverse la relation:
) et
et )

on inverse la relation:
)
+ln(v)=ln(uv))
exponentielle strictement croissante équivaut à

on inverse la relation:
-ln(v)} >0)
ln est donc strictement croissante sur
etc...
voilà quelques indications:
la fonction exponentielle est continue,strictement croissante,jamais nulle,
dérivable de
avec y'=y , y(0)=1, y(a+b)=y(a)y(b).
une relation s'inverse, tout en restant identique à elle-même:
si Pauline est la femme de Jean,Jean est le mari de Pauline.
De même, si x est réel et y>0,
ainsi, chaque fois que tu connais une propriété de l'exponentielle,
tu en déduis une propriété du logarithme népérien:
si
on inverse la relation:
on inverse la relation:
exponentielle strictement croissante équivaut à
on inverse la relation:
ln est donc strictement croissante sur
etc...
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
