X-triangles

[jeancam]

bonjour, un x triangle est un triangle ABC tel que AB^x+BC^x=AC^x
un 1-triangle est donc plat et un 2-triangle rectangle.
disons que l'angle ABC est un x-angle
si quelqu un connait maple peut etre qu il pourrait conjecturer des trucs à propos des x-triangles...

[Clembou]

Pas mal comme piste de recherche :p J'adore ça :++: J'essairais de faire quelques trucs sur ça :we:

[Clembou]

Le sujet m'intéresse fortement. J'ai fais quelques essais avec Geogebra avec comme paramètre :


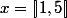
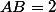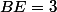cm
cm
et :


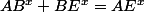
Voici les figures correspondantes :

1-triangle :


2-triangle :


3-triangle :


4-triangle :


5-triangle :


En fait, on conjecture que le côté variable (ici AE) décroit vers la distance (BE) et l'angle décroit jusqu'à atteindre la valeur d'un angle d'un triangle isocèle.

Donc quand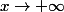 , le x-triangle est un triangle isocèle.

[nuage]

Salut,
Le problème est qu'en général la donnée de ne défini pas l'angle

[nuage]

Donc quand, le x-triangle est un triangle isocèle.

je ne crois pas :
disons que l'on place les points A et C de coordonnées (-1/2,0) et (1/2,0)
Le point B est sur la courbe d'équation

Une étude qualitative rapide, et peut-être fausse, me fais croire que l'angle va varier tout le long de la courbe, entre et

[Clembou]

Ok ! Ce n'était que des résultats qu'il fallait vérifier.

C'est une très grande précision que tu nous donnes là :++:

[nuage]

Mais je te conseille de vérifier mes calculs.

[Clembou]

Mais je te conseille de vérifier mes calculs.

Ok ! Peut-être pas maintenant parce que là je vais me coucher

Bonne nuit :++:

[L.A.]

Bonjour.

Est-ce que il existe des x-angles pour tout x dans R ?

pas pour x=0 déjà

ensuite, les x-angles sont stables par homothétie
Si on raisonne sur des triangles isocèles en A, supposons AB=AC=1
AB^x+AC^x = BC^x = 2 donc BC = 2^(1/x)

l'inégalité triangulaire implique 0<=BC<= 2 donc x>=1 ou x<0

donc il existe des x-angles (isocèles) pour ces valeurs.
Un sujet intéressant, ma foi.

Un triangle equilatéral n'est jamais un x-angle. Mais du coup pour un triangle donné, existe-t-il x tel qu'il soit un x-angle?

[nuage]

Salut,
pour un triangle non isocèle il existe 2 valeurs de x qui conviennent.
L'une est supérieure à 1, l'autre négative.

Disons que les côtés du triangle sont avec
ou
avec