Le nombre de solutions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dame
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Mai 2008, 14:12
-
 par dame » 20 Jan 2009, 15:25
par dame » 20 Jan 2009, 15:25
trouver le nombre de solutions de:
x^2-y^2=2^100
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Jan 2009, 15:47
par Nightmare » 20 Jan 2009, 15:47
A vue de nez je dirai une infinité... Peut être cherches-tu les solutions entières?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 20 Jan 2009, 19:48
par leon1789 » 20 Jan 2009, 19:48
il me semble que x²-y² = (x-y)(x+y)

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 20 Jan 2009, 21:45
par fourize » 20 Jan 2009, 21:45
bonjour;
Nightmare a écrit:Peut être cherches-tu les solutions entières?
je dirais idem, car il est bien vrai que
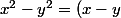(x+y))
mais l'équation n'était pas égale à 0, mais de
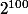
; au finale,
je ne vois pas trop ou ça nous mene :hum:
* In God we trust, for all others bring data *
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Jan 2009, 21:52
par Nightmare » 20 Jan 2009, 21:52
Il s'agit de déterminer tous les x et y tels que :

avec m et k entiers et de somme 100.
-
dame
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Mai 2008, 14:12
-
 par dame » 21 Jan 2009, 15:35
par dame » 21 Jan 2009, 15:35
desole, les solutions dans L'ensemble IN
-
dame
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Mai 2008, 14:12
-
 par dame » 22 Jan 2009, 19:07
par dame » 22 Jan 2009, 19:07
!!!!!!!!!!!!!!!!!!!!!
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Jan 2009, 19:20
par Zweig » 22 Jan 2009, 19:20
Pour déterminer le nombre de couples
)
solution, cela revient à déterminer le nombre d'entiers naturels
)
, que l'on note

, tel que
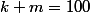
(d'après le message de Nightmare). Un argument combinatoire nous donne ce résultat rapidement :
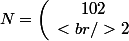 = \frac{102!}{2!\cdot 100!})
Les solutions sont alors
 = \left(2^{k-1}+2^{m-1},2^{k-1}-2^{m-1}\right))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
