Hey! Bonjour à tous! Un petit problème qui doit vmt être bateau, mais j'ai une equation différentielle de premier ordre telle que : xy' - 2y = Sqrt(x)
Bon normalement je connais les techniques pour résoudre ce type d'équations, mais ya un espèce de x qui multiplie ma dérivée de y qui m'embête au plus au point! Car j'avais pensé divisé l'équation par x, et donc résoudre normalement l'équation...mais il existe la possibilité que x = 0, je ne peut donc pas faire ca, de plus on nous donne la condition : y(0) =3.
Donc ca remonte à l'année dernière ce type d'exos, et je ne sais plus tp comment résoudre ca...
Merci d'avance! ;)
EquaDiff!
9 messages
- Page 1 sur 1
Bonjour,
premièrement, tu résous : xy' - 2y = 0
Ensuite tu ajoutes aux fonctions obtenues une solution particulière de xy' - 2y = Sqrt(x)
Pour trouver une solution particulière : soit par intuition ou par tatonnement soit, si on n'a pas réussi, on applique la méthode "de la variation de la constante" qui marche à tous les coups;
premièrement, tu résous : xy' - 2y = 0
Ensuite tu ajoutes aux fonctions obtenues une solution particulière de xy' - 2y = Sqrt(x)
Pour trouver une solution particulière : soit par intuition ou par tatonnement soit, si on n'a pas réussi, on applique la méthode "de la variation de la constante" qui marche à tous les coups;
mais ca, c'est la technique normal, mais je ne sais que l'appliquer sur des equations de types : y'(t) + p(t)y(t) = f(t)... avec comme solution homogène Lambda*exp(-P(t)) et solution générale : y0(t) + Lambda*exp(-P(t))
et non sur celle de type :
a(t)y'(t) + p(t)y(t) = f(t)
Je ne sais pas quoi faire de la fonction a(t) devant ma dérivée de y...
et non sur celle de type :
a(t)y'(t) + p(t)y(t) = f(t)
Je ne sais pas quoi faire de la fonction a(t) devant ma dérivée de y...
je suis bien d'accord avec toi, mais pose x = 0 ! dans ce cas, ta division est impossible! Donc je me suis pas démonté et je suis allé voir un de mes profs... il ma dit tout de suite que la consigne était fausse du fait que si x = 0 --> 0*y'(0) - 2y(0) = sqrt(0)
--> y(0) = 0 !!! et donc du coup leur condition y(0) = 3 est de toute façons impossible! ^^
Merci bien à ceux qui ont essayé!
Tchuu
--> y(0) = 0 !!! et donc du coup leur condition y(0) = 3 est de toute façons impossible! ^^
Merci bien à ceux qui ont essayé!
Tchuu
Salut EZ3kiel ,
l'équation est

a-priori, on a envie de résoudre sur
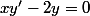
d'où

Pour chercher une solution particulière, on fait "varier" la constante K
on cherche donc une solution particulière sous la forme=K(x)x^2)
d'où
=x^{ -\frac{5}{2}})
d'où=-\frac{2}{3} {x^{ - \frac{3}{2}})
d'où la solution générale:

On voit que toutes les solutions (quelque soit la constante C)
admettent un prolongement par continuité en
Cordialement,
l'équation est
a-priori, on a envie de résoudre sur
d'où
Pour chercher une solution particulière, on fait "varier" la constante K
on cherche donc une solution particulière sous la forme
d'où
d'où
d'où la solution générale:
On voit que toutes les solutions (quelque soit la constante C)
admettent un prolongement par continuité en
Cordialement,
Bonjour EZ3kiel,
Premièrement :
dans ton post d'hier 13h20, tu as écrit :
<< ca, c'est la technique normal, mais je ne sais que l'appliquer sur des equations de types : y'(t) + p(t)y(t) = f(t)... >>
Ton équation est : y'(t)+(-2/t)y(t) = 1/sqrt(t)
C'est bien une équation du type que tu sais résoudre avec p(t) = -2/t et f(t)=1/sqrt(t)
Alors si tu sais appliquer la technique, applique là !!! Qu'est-ce que tu attends pour le faire ?
Deuxièmement :
Dans ton post de 15h48, tu as écrit :
<>
Tu as détecté une difficulté dans le cas particulier où x=0. Très bien de l'avoir noté. Mais qu'est-ce qui t'empèche de résoudre d'abord le problème dans les autres cas où il n'y a pas de difficulté, c'est à dire x>0 ?
Ensuite, il sera toujours temps d'étudier plus précisément de quoi il retourne dans le cas particulier x=0. Et même si tu ne trouves pas la réponse pour x=0, au moins tu ne resteras pas avec une page blanche. C'est trop facile de dire "je saurais faire dans le cas général, mais je ne fais rien parce qu'il y a un cas particulier qui m'embête ".
Allons, ne prends pas mal ces conseils... et bon travail !
Premièrement :
dans ton post d'hier 13h20, tu as écrit :
<< ca, c'est la technique normal, mais je ne sais que l'appliquer sur des equations de types : y'(t) + p(t)y(t) = f(t)... >>
Ton équation est : y'(t)+(-2/t)y(t) = 1/sqrt(t)
C'est bien une équation du type que tu sais résoudre avec p(t) = -2/t et f(t)=1/sqrt(t)
Alors si tu sais appliquer la technique, applique là !!! Qu'est-ce que tu attends pour le faire ?
Deuxièmement :
Dans ton post de 15h48, tu as écrit :
<
Tu as détecté une difficulté dans le cas particulier où x=0. Très bien de l'avoir noté. Mais qu'est-ce qui t'empèche de résoudre d'abord le problème dans les autres cas où il n'y a pas de difficulté, c'est à dire x>0 ?
Ensuite, il sera toujours temps d'étudier plus précisément de quoi il retourne dans le cas particulier x=0. Et même si tu ne trouves pas la réponse pour x=0, au moins tu ne resteras pas avec une page blanche. C'est trop facile de dire "je saurais faire dans le cas général, mais je ne fais rien parce qu'il y a un cas particulier qui m'embête ".
Allons, ne prends pas mal ces conseils... et bon travail !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
