Complexe

par **ultas** » 19 Jan 2009, 19:05

Bonsoir a tous j'aurai besoin de votre aide pour cette exercice.
Alors on a une application f qui a tout point M d'affixe z non nulle associe le point M'=f(M) d'affixe z' tel que [TEX]z'=/frac{z}{mod(z)}*(2-[z])[/TEX ] avec [z] qui signifie module ou valeur absolue de z .On a aussi z=r*e^ia r etant le module de z et a un argument de z.On a aussi [TEX] z'=e^{2-r}[TEX ]
De plus on a pour cette question un point M du plan a l'exterieur du cercle de rayon 1 .On appelle I le milieu du segment [MM'] ou M' est l'image de M par f .
Il faut montrer que I appartient au cercle C1 de rayon 1 et a la demi-droite [OM) .J'ai essaye de calculer l'affixe de I en disant que c'est la somme de l'affixe de M et celui de M' le tout divisé par 2 et j'ai trouve frac{z}{mod(z)} mais je ne suis pas du tout sur de mon resultat.Merci a tous pour votre aide.
--------------------------------------------------------------------------------

par **axiome** » 19 Jan 2009, 19:20

Re,
Tu as le bon résultat pour l'affixe de I :

C'est

.

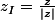
Pour prouver que I appartient au cercle de centre O et de rayon 1, il te suffit de prouver que OI=1.
Calcule donc OI=...=...=1

par **ultas** » 19 Jan 2009, 19:28

Mais il faut les coordonnees de I nn? Comment les trouver a partir de l'affixe??

par **axiome** » 19 Jan 2009, 19:30

Tu as l'affixe de I :

.
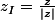
A partir de cela, tu peux calculer OI pour montrer que ça vaut 1.

OI, ça vaut quoi d'après ton cours ?

par **ultas** » 19 Jan 2009, 19:34

desole mais on a pas vu ca dans le cours ou je ne vois pas de koi vou voulez parler

par **axiome** » 19 Jan 2009, 19:36

Bon, je te redonne la formule, mais je pense que tu as mal regardé, elle doit bien se trouver quelque part dans ton cours...

A est d'affixe

et B est d'affixe

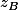
On a :

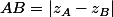
Applique donc cette formule pour OI :

OI= ?

par **ultas** » 19 Jan 2009, 19:42

J'ai applique ca pour 0I J'ai trouve |(-z/|z|)| ce qui ekivo a |-z/z| d'apres le cours (pas sur) ce ki ekivo a |-1|=1

par **axiome** » 19 Jan 2009, 19:48

Oki, mais c'est pas très élégant, marque plutôt :

Calculons :

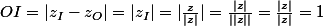
Conclusion :
I appartient au cercle de centre O et de rayon 1.

par **ultas** » 19 Jan 2009, 19:51

Merci bcp pour votre aide mais j'ai besoin de vous pour m'aider a montrer que I appartient a la demi droite [OM) car on a pas du tout vu la geometrie et le nombres complexes

par **axiome** » 19 Jan 2009, 19:56

Montrer que I appartient à la demie-droite [OM), cela revient à démontrer que I et M ont le même argument, OK ?

par **ultas** » 19 Jan 2009, 20:02

Le module de I c'est son affixe ? et comment calculer celui de M

par **axiome** » 19 Jan 2009, 20:08

Bon, on va calculer l'argument de M d'affixe z.
D'abord,
arg(z)= quoi par hypothèse ?

par **ultas** » 19 Jan 2009, 20:10

c'est l'angle entre u est OM??

par **axiome** » 19 Jan 2009, 20:20

Exactement, et il est égal à quoi par hypothèse ?

Complexe

complexe

Qui est en ligne