Dev.lim
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gomaths
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Oct 2007, 13:20
-
 par gomaths » 15 Jan 2009, 21:09
par gomaths » 15 Jan 2009, 21:09
s'il vous plait je cherche à faire ce dl mais ca n' a pas marché
dl à l'ordre n+1 de ln(sigma(k=0)à(n=n)[x^k/k!]
merci
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 15 Jan 2009, 21:34
par XENSECP » 15 Jan 2009, 21:34
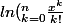)
?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 15 Jan 2009, 21:34
par Clembou » 15 Jan 2009, 21:34
gomaths a écrit:Bonsoir,
s'il vous plait je cherche à faire ce dl mais ca n' a pas marché
dl à l'ordre n+1 de ln(sigma(k=0)à(n=n)[x^k/k!]
merci
Juste une traduction LaTex :
Il faut le DL à l'ordre

de :
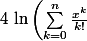)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2009, 21:35
par Nightmare » 15 Jan 2009, 21:35
C'est génial on a un traducteur LaTeX sur le site...
gomaths > Un DL en quel point?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2009, 21:39
par Nightmare » 15 Jan 2009, 21:39
Et humble dans tout ça :lol3:
-
gomaths
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Oct 2007, 13:20
-
 par gomaths » 15 Jan 2009, 21:40
par gomaths » 15 Jan 2009, 21:40
merci pour réponse . le dl en 0
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2009, 21:43
par Nightmare » 15 Jan 2009, 21:43
Dans ce cas là :
Tu remarques que

. Le deuxième terme tend vers 0, il te suffit de faire un DL de ln(1+x) et de composer !
-
gomaths
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Oct 2007, 13:20
-
 par gomaths » 15 Jan 2009, 23:10
par gomaths » 15 Jan 2009, 23:10
merci Nightmare mais sa donne
sigma(k=1)à(k=n)(-1)^(k-1)/k[sigma(i=1)à(i=n)[x^i/i!]]
-
gomaths
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Oct 2007, 13:20
-
 par gomaths » 15 Jan 2009, 23:29
par gomaths » 15 Jan 2009, 23:29
pardon
sigma(k=1)à(k=n)(-1)^(k-1)/k[sigma(i=1)à(i=n)[x^i/i!]^k]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
