AnA92 a écrit:Je dois poster là un autre problème que j'ai eu en nombre complexe:
Résoudre l'équation:
^n=(z+i)^n)
n de IN
Bon voilà la première des chose j'ai remarqué que pour n=0 on a 1=1 donc est ce que la solution est 1 ??
Et aussi pour n=1 on va avoir z-i=z+i => 2i=0 donc pas de solution ou quoi ??
Et pour n>= 2vrmt je ne vois pas quoi faire car à la fin si j'essaie résoudre l'équation par la méthode habituelle je dois avoir :
Je pose z-i=[
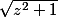
;
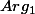
]
et pour z+i=[
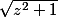
;
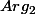
]
donc les mudules sont égaux et pour arg je dois avoir aussi égaux :doh:
Vrmt je ne sais pas quoi faire ??
Quelques remarques...
Si n=0, on obtient bien 1=1, ce qui contrairement aux apparences est toujours une équation en z. Comme ceci est vérifié quel que soit z, l'ensemble des solution est

Si n=1 l'ensemble des solutions est clairement vide, bien sûr !
Pour tout entier n supérieur à 1, on remarque d'abord que i n'est pas solution de cette équation, et ensuite on peut donc diviser les deux membres par
^n)
non ?
A ton avis, cela donne quoi ?
Enfin, je note que poser z-i=[
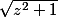
;
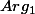
] n'est pas légal, car le module de z-i n'est pas nécessairement
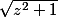
, la première raison étant que
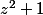
n'est pas nécessairement un réel positif et que par conséquent, il est illégal de simplement écrire
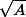
si A n'est pas un réel positif !
