Calcul d'une somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Yavzz
- Membre Naturel
- Messages: 36
- Enregistré le: 12 Oct 2008, 15:33
-
 par Yavzz » 11 Jan 2009, 21:27
par Yavzz » 11 Jan 2009, 21:27
Bonjour, j'aurais besoin d'aide pour le calcul d'une somme :
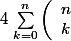 kX^k(1-X)^{n-k})
Des pistes?
Merci d'avance.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Jan 2009, 21:27
par Clembou » 11 Jan 2009, 21:27
Yavzz a écrit:Bonjour, j'aurais besoin d'aide pour le calcul d'une somme :
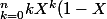^(n-k))
.
Des pistes?
Merci d'avance.
C'est presque le binôme de Newton, non ??
-
Yavzz
- Membre Naturel
- Messages: 36
- Enregistré le: 12 Oct 2008, 15:33
-
 par Yavzz » 11 Jan 2009, 21:28
par Yavzz » 11 Jan 2009, 21:28
oui oui je sais.
Mais le k qui varie dans la somme me pose problème.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Jan 2009, 21:38
par Nightmare » 11 Jan 2009, 21:38
Salut :happy3:
N'y a-t-il pas de coefficients binomiaux?
-
Yavzz
- Membre Naturel
- Messages: 36
- Enregistré le: 12 Oct 2008, 15:33
-
 par Yavzz » 11 Jan 2009, 21:41
par Yavzz » 11 Jan 2009, 21:41
a oui désolé!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Jan 2009, 21:45
par Nightmare » 11 Jan 2009, 21:45
Essaye de dériver
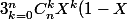^{n-k})
voir ce qu'il se passe!
-
mathelot
 par mathelot » 11 Jan 2009, 21:55
par mathelot » 11 Jan 2009, 21:55
aloha,
grosso modo
calcul de
 = \sum Y^k)
(progression géométrique)
on dérive
 = \sum kY^{k-1})
on multiplie par Y
 = \sum kY^k)
dans la somme initiale, on factorise
^n)
on fait un changement de variable
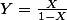
avec coeff binomiaux, même raisonnement en partant de
 = \sum (_k^n) Y^k =(1+Y)^n)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Jan 2009, 21:58
par Clembou » 11 Jan 2009, 21:58
Yavzz a écrit:Bonjour, j'aurais besoin d'aide pour le calcul d'une somme :
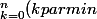 k X^k (1-X)^(n-k))
.
Des pistes?
Merci d'avance.
Edit LaTeX : La formule est la suivante
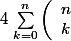 kX^k(1-X)^{n-k})
-
Yavzz
- Membre Naturel
- Messages: 36
- Enregistré le: 12 Oct 2008, 15:33
-
 par Yavzz » 11 Jan 2009, 22:25
par Yavzz » 11 Jan 2009, 22:25
mathelot a écrit:aloha,
grosso modo
calcul de
 = \sum Y^k)
(progression géométrique)
on dérive
 = \sum kY^{k-1})
on multiplie par Y
 = \sum kY^k)
dans la somme initiale, on factorise
^n)
on fait un changement de variable
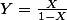
avec coeff binomiaux, même raisonnement en partant de
 = \sum (_k^n) Y^k =(1+Y)^n)
Désole mais je ne comprends pas très bien le déroulement, toutes les explications sont dans le désordre.
Cette aprem, j'avais essayer la dérivation, ça saute aux yeux.
Mais
^{n-k})
fait que lorsqu'on dérive, la somme se scinde en 2 parties, avec des puissances différentes.
En dérivant
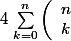 X^k(1-X)^{n-k})
= 1
Je me retrouve avec :
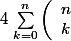 kX^{k-1}(1-X)^{n-1-k} ( k(1-X) + (n-k)X))
= 0
Et là je bloque depuis cette aprem.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 11 Jan 2009, 22:28
par Clembou » 11 Jan 2009, 22:28
Yavzz a écrit:Désole mais je ne comprends pas très bien le déroulement, toutes les explications sont dans le désordre.
Fais comme a dit Nightmare. Dérives la somme...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 11 Jan 2009, 23:52
par Joker62 » 11 Jan 2009, 23:52
Sinon on réécrit le Coeff Binomiale avec sa définition
On simplifie par k
On sort un n
On sort un X
On réajuste la somme
Et on trouve.
-
Yavzz
- Membre Naturel
- Messages: 36
- Enregistré le: 12 Oct 2008, 15:33
-
 par Yavzz » 11 Jan 2009, 23:59
par Yavzz » 11 Jan 2009, 23:59
Sur mon dernier post, je me suis trompé dans le somme.
Mais sinon j'ai repris du début le calcul, et ça semble marcher.
Petite question : lorsque je dérive ma relation
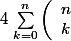 X^k(1-X)^{n-k})
= 1
j'ai bien une somme qui va de k = 1 à n-1?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 12 Jan 2009, 00:03
par Joker62 » 12 Jan 2009, 00:03
Peut-être parce qu'il ne faut pas dériver ? :)
Jette ta feuille et fait le avec ma méthode tu finiras en 5 lignes...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
(progression géométrique)