Les limites, thème : famille de cercles

[celine31]

Bonjour à tous
je suis une élève de 1ère S et je galère quelque peu avec un exo sur les limites et les cercles alors si vous pouviez m'aider ce serait super sympa parce que je suis vraiment perdu

Voici l'enoncé:

f est la fonction définie sur ]-;);0[U]0;+;)[ par f(x)= 1-x + 1/x, C est sa courbe représentative dans un repère orthonormal (O; i, j)

1- a) Prouvez que C admet une asymptote d d'équation y= 1-x
b) Précisez la position de C par rapport à d.

2- a) Etudiez les variations de f et tracez d et C
b) Discutez, suivant les valeurs de m, le nombre de solutions de l'équation f(x)= m

Jusque là ca va j'ai plus ou moins réussi mais c'est après que ca se complique

3- Lorsque la droite d'équation y=m coupe C en deux points distincts M1 et M2, d'abscisses x1 et x2, on note H1 et H2 les points de l'axe des abscisses ayant respectivement la même abscisse x1 et x2 que M1 et M2.

a) Prouvez que x1 et x2 sont solutions de l'equation: x²-(1-m)x-1=0
b) Vérifiez que: H1H2²= (x2-x1)²= (x2+x1)²-4(x1x2), et déduisez-en H1H2² en fonction de m.

4- On note Tm le cercle de diamètre [H1H2].
a) Vérifiez que son centre a pour abscisse (1-m)/2 et que son rayon r est tel que r²= 1 + (1-m)²/4
b) Déduisez-en que x²+y²-(1-m)x-1= 0 est une équation de Tm

5- Construisez le cercle Tm pour m=1, m=2, m=3. Que remarquez-vous? Prouvez-le.


Voila, je vous remercie d'avance de m'aider, je suis vraiment à la ramasse, je n'y comprend vraiment rien, donc voila

Merci beaucoup.

[Quidam]

Pour déterminer les abscisses des points d'intersections de deux courbes et 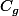représentatives respectivement des fonctions f et g, il suffit de résoudre l'équation f(x)=g(x) !

En effet, si , il est clair que le point appartient à et à 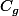. La réciproque est tout aussi évidente !

Ici, tu as qui est appelée C et une fonction g(x)=m. La droite d'équation y=m (appelons-la D) est la courbe représentative de la fonction g(x)=m.

Donc pour trouver les points d'intersection de C et D, il suffit de résoudre l'équation :

f(x)=g(x)

c'est à dire, l'équation : f(x)=m, ce qui donne :



En manipulant un peu cette équation, tu dois tomber sur l'équation équivalente x²-(1-m)x-1=0 qui est demandée !