équation solution imaginaire

par **maria3bx** » 11 Jan 2009, 14:19

bonjour à tous ,

je dois démontrer que (E) a une solution imaginaire pur

(E) = z^3 + (-8+i)z²+(17-8i)z+17i = 0

je sais donc que je dois trouver une solution de la forme z = iy

j'ai pensé mettre en facteur z

z( Z²+iz+17-8i-8z) = 17 i ?? ensuite passer de l'autre côté en divisant ?

par **Yuki91** » 11 Jan 2009, 14:21

mettre z en facteur c'est une bonne idée je pense mais le 17i si tu le passe de l'autre coté sa te fait -17i deja

par **maria3bx** » 11 Jan 2009, 14:26

seulemnt après ça s'embrouille un petit peu

ej trouve que z = ( -17 i) / ( z²-8z+iz+17-8i ) si je fais le conjugé je me retrouve avec un tas de calculs... :hum:

par **Yuki91** » 11 Jan 2009, 14:30

tu ne peut pas faire z=-17i ou z²-8z+iz+17-8i=17i ?

par **marie49** » 11 Jan 2009, 14:36

Non ca c'est faux!

Quand tu as une equation du type a*b=0 alors, a=0 ou b=0, mais par exemple pour a*b=17i tu pourrais avoir a=17 et b=i....
Ca ne marche qu'avec 0!

par **maria3bx** » 11 Jan 2009, 14:38

je ne sais pas je ne vois pas comment je peux arriver a z = iy :triste:

j'ai z( Z²+iz+17-8i-8z) = -17 i
si je dis Z²+iz+17-8i-8z = -17i et que je remet en facteur

z ( z +i-8 )+17 = -17i+ 8i j'ai toujours ce 17 qui me dérange

par **XENSECP** » 11 Jan 2009, 14:46

maria3bx a écrit:bonjour à tous ,

je dois démontrer que (E) a une solution imaginaire pur

(E) = z^3 + (-8+i)z²+(17-8i)z+17i = 0

je sais donc que je dois trouver une solution de la forme z = iy

j'ai pensé mettre en facteur z

z( Z²+iz+17-8i-8z) = 17 i ?? ensuite passer de l'autre côté en divisant ?

Tu cherches z sous la forme

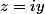
Or on remarque que z = -i est solution donc on factorise par (z+i) :

On a ensuite un trinôme :

Discriminant ... et je te laisse finir ^^

par **marie49** » 11 Jan 2009, 14:48

Une fois que tu as remarqué que -i est solution, l'exercice est terminé en fait!

Tu as trouvé ta solution imaginaire...

par **XENSECP** » 11 Jan 2009, 14:49

marie49 a écrit:Une fois que tu as remarqué que -i est solution, l'exercice est terminé en fait!

Tu as trouvé ta solution imaginaire...

Hum faut voir si l'autre solution (à partir du trinome) ne t'en donne pas une autre (ok ca se voit mais bon

)

par **maria3bx** » 11 Jan 2009, 14:55

hum je trouve donc que le discriminant = - 4 donc x 1 = (8+ (i racine4 ))/2
x 2 = ( 8 - (i racine4)) / 2 ??

par **maria3bx** » 11 Jan 2009, 14:58

enfin enfin 4- i en simplifiant et 4 + i

donc -i = -4 et -i = 4

équation solution imaginaire

équation solution imaginaire

Qui est en ligne