Pb de continuité
14 messages
- Page 1 sur 1
pb de continuité
bonjour à tous, je suis face à un grand problème de continuité :
"déterminer f continue en 0 tq f(x+y) = f(x)f(y) avec x,y réels". Comment faire déjà, je suis complètement novice en fonctions ? J'ai vu que f(nx) = [f(x)]^n, mais aidez-moi si y'a + rapide merci
"déterminer f continue en 0 tq f(x+y) = f(x)f(y) avec x,y réels". Comment faire déjà, je suis complètement novice en fonctions ? J'ai vu que f(nx) = [f(x)]^n, mais aidez-moi si y'a + rapide merci
Bonjour,
tu peux essayer de calculer f(0) (deux valeurs possibles)
que=f(\frac{x}{2}+\frac{x}{2})) est nécessairement positif,
est nécessairement positif,
poser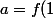)
puis) pour n entier naturel,relatif.
pour n entier naturel,relatif.
utiliser le fait qu'une fraction est une somme

utiliser les puissances fractionnaires, qui, elles, sont définies
comme des fonctions réciproques de fonctions puissances
Montrer que f est continue partout
puis, pour x irrationnel, utiliser le fait que) est de Cauchy
est de Cauchy
si tend vers
tend vers  .
.
tu peux essayer de calculer f(0) (deux valeurs possibles)
que
poser
puis
utiliser le fait qu'une fraction est une somme
utiliser les puissances fractionnaires, qui, elles, sont définies
comme des fonctions réciproques de fonctions puissances
Montrer que f est continue partout
puis, pour x irrationnel, utiliser le fait que
si
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
