Formes différentielles

[aurk]

Bonjour,

j'ai un exercice de maths où la question est calculer les différentielles extérieures des formes différentielles suivantes: w1= 2xy dx + x² dy.

Je necomprend pas la question, que faut-il faire exactement? Faut-il calculer l'intégrale? C'est ce que je pensais au début mais il n'y a pas d'intervalle pour intégrer.

Pouvez-vous m'aider s'il vous plaît? Merci

[busard_des_roseaux]

Bonjour,

j'ai un exercice de maths où la question est calculer les différentielles extérieures des formes différentielles suivantes: w1= 2xy dx + x² dy.

Je ne comprend pas la question, que faut-il faire exactement? Faut-il calculer l'intégrale? C'est ce que je pensais au début mais il n'y a pas d'intervalle pour intégrer.

Pouvez-vous m'aider s'il vous plaît? Merci

Ta différentielle ne semble pas "extérieure" :doh:
Elle est exacte,ie,

w1=dw

où


On voit mieux quel genre d'objet est w1
il s'agit d'une application de


dans le dual (topologique) de
ie, une combinaison linéaire de deux coordonnées, les polynômes
étant ses coordonnées dans la base duale.

dx:

est la même application que l'application "1ere coordonnée":



PS: il me semble qu'une forme différentielle fermée, définie sur un ouvert
simplement connexe est exacte (apprendre son cours :zen: )
et que l'on peut intégrer la 1ère coordonnée qui est un


le long d'un lacet de à

Là, ce n'est pas la peine de se fatiguer car la primitive est évidente.

L'intéret de ce binzz, c'est que le dual fournit un espace vectoriel,
formé de combinaisons linéaires d'accroissemnt finis dans , ce qui n'a pas trop d'intéret, mais ensuite, si l'on a décrit
une surface S, un volume V ou une variété X, les cartes que constituent les
différents paramétrages de la surface ou de la variétés vont envoyer tangenciellement à cette surface, les accroissements numériques de
Si tu as envie de voir ce qui se passe sur un exemple simple, fais de la
géométrie sur des triangles sphériques et retrouve localement
le théorème de Pythagore.

Quant à l'algèbre extérieure, c'est la même chose mais avec des déterminants
mineurs (formes p-linéaires alternées) en lieu et place des différentielles.

[quinto]

Salut,

il me semble qu'une forme différentielle fermée, définie sur un ouvert
simplement connexe est exacte

le théorème usuel dit que ca doit etre vrai sur un ouvert étoilé, cependant tout le monde, moi y compris l'utilise sur un domaine simplement connexe, je l'ai peut être démontré en exercice il y'a fort longtemps. A t'on vraiment le droit de le faire sur un simplement connexe non étoilé ? Si oui qu'est ce qui permet de passer de l'un à l'autre ?

[busard_des_roseaux]

re,


je regarde mon vieux Cartan "calcul différentiel" chez Hermann.

L'intégrale ne dépend que de la classe d'homotopie de si est fermée.

si n'est pas fermée, ce n'est pas nécéssairement le cas.
L'intégrale dépend du représentant choisi.

maintenant si l'ouvert est simplement connexe, tous les chemins allant
du point au point sont dans la même classe
d'homotopie.

Il suffit de considérer
l'exemple suivant:
Soit l'argument d'un nombre complexe:


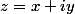
la forme trigo de z donne
+ constante
dans un ouvert qui ne rencontre pas l'axe y'oy.

on peut donc calculer la différentielle de la fonction de deux variables



est fermée. Son intégrale sur un lacet compte le nombre de tours (en radians) que fait autour de l'origine O du plan complexe privé de O.

[aurk]

Bonjour, bonne année et merci pour vos réponses,

voilà seulement que je peux voir vos réponses, c'est pourquoi j'ai été si longue.

je vais regarder tout cela aujourd'hui et demain.