Complexes - TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 03 Jan 2009, 12:55
par lilou942 » 03 Jan 2009, 12:55
Bonjour,
J'ai un exo sur les complexes où je bloque à la dernière question :Soit z n nombe complexe différent de i. On posera z= x + iy.
Soit z'= x'+iy'=

.
Soit M, le point d'affixe z et M' le point d'affice z'.
1) Calculer x' et y' en fonction de x et y.Je trouve x'=
^2})
et y'=
^2})
.
2) Déterminer l'ensemble des points M tels que z' soit un nombre réel.Je trouve un cercle de rayon

et de centre (-2;
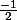
).
3) On pose Z= z -i et Z'= z' -i.
a) Montrer que ZZ'= -3+ 4i. Calculer alors |ZZ'|.Je trouve |ZZ'|=5.
b) Prouver que si M appartient à un cercle de centre A d'affixe i et de rayon r alors M' appartient aussi à un cercle de centre A. Déterminer r pour que les deux cercles soient égaux.Ici je ne sais pa par quoi commencer..
Pourriez vous vérifiez mes résultats et m'aider pour la question 3)b)?
Merci d'avance.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 03 Jan 2009, 12:57
par XENSECP » 03 Jan 2009, 12:57
Tu as trouvé que M appartient à un cercle de centre A ?
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 03 Jan 2009, 13:26
par lilou942 » 03 Jan 2009, 13:26
Bah j'ai trouvé que l'ensemble des points M est un cercle mais montrer que ce cercle appartient à un autre cercle de centre A, c'est montrer que cet ensemble de points a pour centre A ?
... Je sais pas comment faire
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 03 Jan 2009, 13:30
par XENSECP » 03 Jan 2009, 13:30
oui c'est bon je vois ^^
Alors en fait comme |ZZ'| = 5, si M appartient à un cercle de centre A tel que A est d'affixe i, et que le cercle est de rayon r alors c'est que |Z| = r.. Tu en déduis |Z'| = .. et le cercle de centre A ;)
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 04 Jan 2009, 20:31
par lilou942 » 04 Jan 2009, 20:31
Euuh, moi je ne vois pas ? :hein:
Pourquoi |Z| serait égal à r ?
Merci d'avoir répondu et de m'éclairer ^^
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 04 Jan 2009, 21:38
par lilou942 » 04 Jan 2009, 21:38
En fait que vaut concrètement |ZZ'| ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Jan 2009, 21:41
par XENSECP » 04 Jan 2009, 21:41
Concrètement ? Lol ! Pas grand chose !
Tu supposes que |Z| = r et tu en déduis le module de |Z'| ;)
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 04 Jan 2009, 22:21
par lilou942 » 04 Jan 2009, 22:21
Donc si on pose |Z|= r ; ça équivaut à |Z'|= 5/ r ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Jan 2009, 22:50
par XENSECP » 04 Jan 2009, 22:50
Voilà ;) Donc tu en déduis le 2ème cercle ;)
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 05 Jan 2009, 07:26
par lilou942 » 05 Jan 2009, 07:26
Okayy^^
Donc r= 2, les deux cercles sont égaux.
Mais comment prouver que si M appartient à un cercle de centre A d'affixe i et de rayon r alors M' appartient aussi à un cercle de centre A ?
Merci
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 05 Jan 2009, 08:17
par XENSECP » 05 Jan 2009, 08:17
C'est ce qu'on vient de chercher à calculer !!!
Et non r n'est pas égal à 2 pour que ce soit le même cercle ^^
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 05 Jan 2009, 19:11
par lilou942 » 05 Jan 2009, 19:11
r=
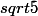
?
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 05 Jan 2009, 19:31
par lilou942 » 05 Jan 2009, 19:31
Car si |z'|= 5/r et |z|= r
Pour que les deux cercles soient égaux , ils faut qu'ils aient le même rayon et donc que |z|=|z'| ce qui équivaut à r =
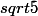
-
lilou942
- Membre Relatif
- Messages: 165
- Enregistré le: 24 Déc 2005, 11:22
-
 par lilou942 » 05 Jan 2009, 21:58
par lilou942 » 05 Jan 2009, 21:58
C'est bien racine de 5 ? :hein:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
