Bonjour,
N'ayant rien trouvé dans la littérature, Je fais appel au forum pour avoir la solution à mon problème que je ne suis pas en mesure de résoudre (je ne suis pas étudiant et j'ai besoin de la solution pour une application professionnelle).
Soit un cercle de diamètre D
La corde AB délimite un segment de cercle
La corde AB est horizontale et sa position est définie par la cote H qui peut varier de 0 à D
La surface du segment peut être calculée par la formule suivante:
S=D/2*[D/2*(arc cos(1-2*H/D))-(D/2-H)*sin(arc cos(1-2H/D))]
Pour:
H=0 ; S=0
H=D/2 ; S= A/2
H=D ; S=A
A étant l'aire du cercle
Problème:
Connaissant la surface du segment et le diamètre du cercle peut on exprimer de la même façon la cote H en fonction de S et de D
Application:
Un réservoir cylindrique en position horizontale contient un volume de liquide
Connaissant S quelle est la hauteur H du liquide?
Merci pour votre aide même si ma demande n'est pas conforme à l'éthique du site.
Hauteur d'un segment de disque
4 messages
- Page 1 sur 1
Bonjour( :we: ),
Est-ce qu'il faut a tout prix avoir la solution sous forme analytique?
Parce que si il faut juste une valeur, on peut remarquer que S(h) est strictement croissante donc elle admet une bijection réciproque) . Autrement dit a chaque
. Autrement dit a chaque  , s étant l'aire d'une surface, correspond une unique hauteur h.
, s étant l'aire d'une surface, correspond une unique hauteur h.
On peut procéder par dichotomie par exemple pour trouver h.
Est-ce qu'il faut a tout prix avoir la solution sous forme analytique?
Parce que si il faut juste une valeur, on peut remarquer que S(h) est strictement croissante donc elle admet une bijection réciproque
On peut procéder par dichotomie par exemple pour trouver h.
la vie est une fête 
Bonjour,
A ce jour j'ai tester deux méthodes
1_ L'utilisation du solveur (valeur cible) dans un tableur. Mais je souhaitais m'affranchir de l'utilisation d'une macro visual basic.
2_ Autre essai, J'ai posé:
S=K*D²
La valeur de K varie de 0 à Pi/4
A l'aide d' un tableur j'ai tracé la courbe K=f(H/D)
puis calculer la polynomiale (ordre 6) correspondant à la courbe
Les résultats obtenus sont acceptable pour 0.1<H/D<1 (erreur < 1% sur le calcul de S)
Le but de ma demande est de savoir s'il est possible de formuler H en fonction de S et de D telle que l'expression ci dessus de S fonction de H et de D.
Merci
A ce jour j'ai tester deux méthodes
1_ L'utilisation du solveur (valeur cible) dans un tableur. Mais je souhaitais m'affranchir de l'utilisation d'une macro visual basic.
2_ Autre essai, J'ai posé:
S=K*D²
La valeur de K varie de 0 à Pi/4
A l'aide d' un tableur j'ai tracé la courbe K=f(H/D)
puis calculer la polynomiale (ordre 6) correspondant à la courbe
Les résultats obtenus sont acceptable pour 0.1<H/D<1 (erreur < 1% sur le calcul de S)
Le but de ma demande est de savoir s'il est possible de formuler H en fonction de S et de D telle que l'expression ci dessus de S fonction de H et de D.
Merci
S=D/2*[D/2*(arc cos(1-2*H/D))-(D/2-H)*sin(arc cos(1-2H/D))]
Posons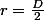
1-2H/D est strictement decroissante sur [0;D] et comprise entre -1 et 1 donc on peut poser
=1-\frac{2H}{D}=1-\frac{H}{r}<br />\Leftrightarrow H=r(1-cos(\alpha))=r+rcos(\alpha))
On peut au moins simplifier S:
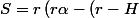sin(\alpha)\right )\\<br />S=r(r \alpha+\frac{sin(2\alpha)}{2}))
Je pense pas qu'on puisse expliciter par des fonctions usuelles mais peut etre que je me trompe
par des fonctions usuelles mais peut etre que je me trompe
Posons
1-2H/D est strictement decroissante sur [0;D] et comprise entre -1 et 1 donc on peut poser
On peut au moins simplifier S:
Je pense pas qu'on puisse expliciter
la vie est une fête 
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
