Bonjour,
J'ai des difficultés de trouver l'intervalle de la fonction suivante:
f(x)=arccos(x^2-1)
J'ai commencé avec l'intervalle de cos(x) est entre [0,Pi]
mais comment est-ce qu'on peut calculer l'intervalle de cos(x^2-1) ?? :briques:
Après ca, j'ai pu trouver l'intervalle de f(x) tel que f(I)=J...
Merci en avance
Analyse fonction arccosinus
10 messages
- Page 1 sur 1
On a trouvé auparavant que Df=Dg.
En dérivant f et g sur Df, on a
=g'(x))
Donc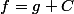 or
or =g(0)\ge C=0) donc
donc 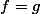
Maintenant, si je passe pas par la dérivée, mais par cos :
on a toujours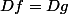
)=h(x)\\<br />cos(g(x))=h(x)\\<br />\text{ avec } h(x)=x^2-1)
On retrouve:
)=cos(g(x)))
donc=g(x)+2k\pi)
Or=g(0)) donc
donc 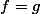
Mais du coup, vu qu'on doit préciser l'ensemble de definition de g et f, ca revient a résoudre l'exo sans pour autant se servir de g (vu qu'on veut juste calculer l'ensemble de définition). Ou alors j'ai raté quelquechose
En dérivant f et g sur Df, on a
Donc
Maintenant, si je passe pas par la dérivée, mais par cos :
on a toujours
On retrouve:
donc
Or
Mais du coup, vu qu'on doit préciser l'ensemble de definition de g et f, ca revient a résoudre l'exo sans pour autant se servir de g (vu qu'on veut juste calculer l'ensemble de définition). Ou alors j'ai raté quelquechose
la vie est une fête 
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
