Continuité

[tomito]

Bonjour
j'aimerai avoir une aide concernant un exercice sur la continuité
soit f Q vers Q la fction caractériqtique de Q , c'est à dire definie ainsi
f(x) =1 si x appartient à Q et 0 sinon

Comment montrer que f nest continue en aucun point de R.?
et que dire de la continuité de g def sur R par g(x)=x*f(x)?
et j'ai une autre question qui est incomprehensible sur les limites
et merci d'avance

[Antho07]

Une foncton continue f est continue en a si et seulement pour toutes suites convergeant vers a alors

converge vers f(a).

Autrement dit si il existe une suite u qui converge vers a et tels que f(u) ne converge pas vers f(a) alors f n'est pas continue en a.


Dans ton cas

Soit x dans R

1er cas: x est rationnel , on sait qu'il existe une suite .....


2eme cas: x irrationnel, on sait qu'il existe une suite.....

[tomito]

je vois toujours pas
la relation entre la suite et les rationnels

[Antho07]

Tout réel est limite ......

[Antho07]

Ou encore

Q est .... dans R ?



Vois-tu de quoi je parle ou pas du tout?

Ou alors on peut aussi formuler comme ça:

Dans tout intervalle de R (non reduit à un singleton), on peut trouver un ....

[tomito]

ca j'ai compris mais je vois pa comment sen servir pour prouver qu'il n'a ya pa continuité
et cett efonction n'est elle pas continue en 1 ?

[Antho07]

Tu as compris quoi?

[tomito]

j'ai compris qu il falait distinguer les cas

[Antho07]

d'accord mais l'élement essentiel de la preuve du résultat ennoncé dans cet exercice c'est pas ça.



Q est dense dans R , est-ce que cela te dit quelque chose?

[tomito]

non ca ne me dit rien

[Antho07]

Dans tout intervalle de R (non reduit à un singleton), on peut trouver un rationnel .

cela te dit quelque chose?

[tomito]

oui mais sa sert à quoi pour lexercice?

[Antho07]

Ok donc tu as vu que dans tout intervalle ouvert de R non vide, il y avait un rationnel ? (oui non)
(la meme chose que ce que j'ai écris plus haut mais pour eviter d'avoir à exclure les intervalle du type [a;a] )


Bon alors après
soit x dans R

alors pour tout n entier il existe un rationnel dans



clairement (par le theroeme des gendarmes) la suite tend vers x.
Or la suite est une suite composé uniquement de rationnels.


Ceci montre que tout réel est limite d'une suite de rationnels.

(On dit que Q est dense dans R)


Alors maintenant , pour revenir à l'exercice.
Soit x dans R
si x est irrationel, il existe une suite de rationnels qui converge vers x.

Soit cette suite.

On a

mais pour tout n, donc

donc

cependant x lui est irrationel donc

Conclusion
donc f n'est pas continue en x.


Le cas x irrationnel est réglé.



Pour le cas x rationnel, il faut se servir de:


Dans tout intervalle ouvert non vide, il existe un irrationnel

autrement tout réel est limite d'une suite d'irrationnels

[Antho07]

En gros cet exercice repose sur

- f:I-->R
"f continue en a" équivalent à "pour tout suite u à valeur dans I convergeant vers a , la suite f(u) converge vers f(a)"

(continuité equivalent à continuité séquentielle)

-Densité de Q dans R

- Densité de (R\Q) dans R


Si tu as compris ces 3 points, l'exercice ne devrait pas poser de probleme

[Antho07]

Pour la question 2, sauf erreur la fonction g est continue en un seul point...

[tomito]

merci pour ton aide
je vois très bien maintenant
mon problème c'était que je ne savais pas me servir des suites pour prouver une continuité
pour la deuxième question il faut suivre le même raisonnement?

[Antho07]

à un détail près. Il y a un point où g est continue.

[tomito]

jpense que c'est zero mais je sais pas le montrer

[Antho07]

oui g est continue en 0. On va essayer avec les suites

Il faut montrer que pour toutes suites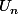 tendant vers 0 , alors tend vers g(0)=0


Soit convergeant vers 0

Je pense qu'on peut faire comme ça.

On va distinguer 2 cas:

-La suite stationne vers 0 (devient =0 à partir d'un certain rang) alors .....

-La suite ne stationne pas vers 0.
Elle prend donc une infinité de valeurs

-Elle prend
~soit une infinité de valeurs rationnels et un nombre fini de valeur irrationnels: C'est à dire qu'elle est rationnel à partir d'un certain rang donc ....

~soit une infinité de valeurs irrationnelles et un nombre fini de valeur rationnelle. C'est à dire qu'elle devient irrationnel à partir d'un certain rang donc...

~soit une infinités de valeurs rationnelles, soit une infinité de valeurs irrationnelles. Dans ce cas, on peut extraire deux sous-suites. Une sous-suite comprenant toutes les valeurs rationnelles de la suite 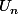et une sous-suite comprenant toutes les valeurs irrationnelles de la suite .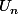

En raisonnant sur ces deux sous-suites et en montrant que tend vers 0 et tend vers 0, on peut montrer qu'alors tend vers 0. On doit pouvoir conclure comme ça je pense.



Après il y a peut etre plus simple, mais à premiere vue je ferais comme ça.


EDIT:désolé pour mon manque de rigueur pour l'écriture des suites