Exponentielle et géométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adel7604
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2007, 13:08
-
 par adel7604 » 02 Jan 2009, 16:28
par adel7604 » 02 Jan 2009, 16:28
Bonjour à tous , j'ai un compte rendu d'un Tp a faire et je bloque sur une demonstration :
On considere les courbes C1 et C2 d'équations respectives y=exp(x) et y=exp(-x) dans un repere orthonormal (O,u,v) du plan. Soit a un nombre réel quelconque. On désigne respectivement par M et N les points de C1 et C2 d'abscisse a par (T1) et (T2) les tangentes à C1 et C2 en M et N. Les droites (T1) et (T2) coupent respectivement l'axe des abscisses en P et Q.
1-a/ Donner l'équation réduite des droites (T1) et (T2) en fonction de a.
yT1=exp(a)(1+x-a)
yT2=exp(-a)(1-x+a)
b/Verifier que le produit de leur coefficient directeur est -1
exp(a) x [-exp(-a)] = -exp(0)= -1
c/Démontrer la conjecture émise . La conjecture est que quelque soit la valeur du réel a , la longueur de segment [PQ] est toujours le même.
Je ne vois pas comment démontrer cette conjecture
Mercie d'avance pour ceux qui vont m'aider
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2009, 16:33
par XENSECP » 02 Jan 2009, 16:33
OK alors déjà on sait que l'abscisse de P et Q est toujours nul donc le segment PQ est de longueur : yP-yQ (en valeur absolue).
P est le point d'intersection entre T1 et la droite x=0, donc tu en déduis l'ordonnée de P et idem pour Q :)
-
adel7604
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2007, 13:08
-
 par adel7604 » 02 Jan 2009, 16:40
par adel7604 » 02 Jan 2009, 16:40
ok merci mais je comprends pas que se soit toujours l'abscisse qui soit nul j'aurai dit plutôt que c'était l'ordonnée donc je ne comprend pas trop !!!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2009, 16:41
par XENSECP » 02 Jan 2009, 16:41
Pardon ^^ J'ai mal lu ;)
Autant pour moi :) Tu fais le même raisonnement avec yP=yQ=0 et xP et xQ à déterminer ;)
-
adel7604
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2007, 13:08
-
 par adel7604 » 02 Jan 2009, 16:50
par adel7604 » 02 Jan 2009, 16:50
ce n'est rien !!!
Faut-il faire ceci :
Pour le point P son abscisse est : 0 = exp(a)(x-a) + exp(a)
Pour le point Q son abscisse est : 0 = -exp(-a)(x-a) + exp(-a)
?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2009, 17:26
par XENSECP » 02 Jan 2009, 17:26
Oui et tu dois calculer xP-xQ !
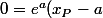 + e^{a} e^{a} = e^{a} (a - x_{P}) a - x_{P} = 1)
Idem pour xQ ...
Dis moi quand tu auras fini

-
adel7604
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2007, 13:08
-
 par adel7604 » 02 Jan 2009, 17:30
par adel7604 » 02 Jan 2009, 17:30
pour xp je trouve -1+a et pour xq je trouve 1+a
ensuite j'ai fait : xq-xp= 1+a---1+a) = 2
-
adel7604
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2007, 13:08
-
 par adel7604 » 02 Jan 2009, 17:31
par adel7604 » 02 Jan 2009, 17:31
dsl je me suis trompée en écivant
xq-xp =1+a-(-1+a) =2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
