Inéquation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AlleinLink
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Jan 2009, 15:27
-
par AlleinLink » 02 Jan 2009, 13:32
Bonjour, bonjour! Je dois montrer que pour tout entier n: 2^n > n
Je l'ai d'abord fait par récurrence:
. Pour tout n;)0, 2^n>0
. Puis par récurrence, pour n=1, 2>1 ca marche.
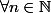
+/0
2^(n+1)=2x2^n
Or 2^n>n
2^(n+1)>2xn
2^(n+1)>n+1
CQFD
Est ce bon?
Apres il faut le montrer à l'aide du binome de Newton et je bloque:
2^n=(1+1)^n=
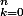
k parmi n
=
! k!})
Et après que faire?
Merci d'avance!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
par XENSECP » 02 Jan 2009, 13:37
problème de TEX ^^
Pour la récurrence ça me va, pour n>1, 2n>n+1
Pour le binôme... je suppose qu'il faut démontrer que 2^n = somme(...) ?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
par Antho07 » 02 Jan 2009, 13:44
AlleinLink a écrit:Apres il faut le montrer à l'aide du binome de Newton et je bloque:
2^n=(1+1)^n=
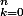
k parmi n
=
La formule de "k parmis n" est fausse.
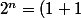^{n} =\bigsum_{k=0}^{n} \begin{pmatrix}n\\k \end{pmatrix} =\bigsum_{k=0}^{n} \frac{n!}{(n-k)!k!})
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
par Antho07 » 02 Jan 2009, 14:01
Ensuite on peut écrire
^{n}=\bigsum_{k=0}^{n} \begin{pmatrix}n\\k \end{pmatrix}=\begin{pmatrix} n \\1 \end{pmatrix} + \begin{pmatrix} n \\n-1 \end{pmatrix} +\left(1+\bigsum_{k=2}^{n-2} \begin{pmatrix} n\\k \end{pmatrix} \right))
EDIT: j'ai montré plus compliqué ... tant pis (j'etais pas partis sur le bon truc à montrer)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
