Suite arithmétique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 00:15
par viina » 31 Déc 2008, 00:15
dans mon DM, j'ai une question qui me bloque.
On me donne :
U1 = 14 000 et r = -950
Etablir l'expression de Un en fonction de n .?
je ne sais pas du tout comment le calculer =X
Peu être à partir de :
Un = U1 (n-1) r
mais apres je ne sais pas le calculer :S
pouvez vous m'aider ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 00:16
par Billball » 31 Déc 2008, 00:16
suite arithmétique je présuppose?
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 00:30
par viina » 31 Déc 2008, 00:30
Billball a écrit:suite arithmétique je présuppose?
oui

peux tu m'aider ?

-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 00:31
par Billball » 31 Déc 2008, 00:31
au rang Uo, que vaut Un?? et quel est le terme général d'une suite Un?
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 00:32
par viina » 31 Déc 2008, 00:32
euh ... rien ? xD U0 c'est rien non ?
le terme général de Un ? =S oula
euh je dirai
Un = U1 (n-1) r ??? ou non peu être pas..
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 00:35
par Billball » 31 Déc 2008, 00:35
viina a écrit:euh ... rien ? xD U0 c'est rien non ?
si je me suis mal fait comprendre! que cherche tu dans ton expression?
tu sais que si la suite est arithmétique :
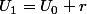
donc...
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 00:39
par viina » 31 Déc 2008, 00:39
Billball a écrit:si je me suis mal fait comprendre! que cherche tu dans ton expression?
tu sais que si la suite est arithmétique :
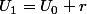
donc...
je cherche a établir Un en fonction de n
donc euh..
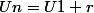
... ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 00:42
par Billball » 31 Déc 2008, 00:42
viina a écrit:je cherche a établir Un en fonction de n
donc euh..
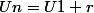
... ?
nan ca c faux ^^
à un rang n quelconque :
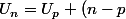r)
au rang 1 connaissant

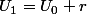
par de là et tu trouveras ce que tu veux!
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 31 Déc 2008, 00:42
par Clembou » 31 Déc 2008, 00:42
Non ! Déjà essaie de calculer

. Ensuite, tu pourras trouver la formule qui te permet d'avoir

en fonction de

et de

.
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 00:52
par viina » 31 Déc 2008, 00:52
je ne comprend plus rien, déja que j'ai du mal de base (lol).
En faite, je ne comprend pas pourquoi U0 ? c'est en fonction de n.
l'énoncé : Etablir l'expression de Un en fonction de n.
donc je dois, je pense, trouver la formule de Un.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 00:54
par Billball » 31 Déc 2008, 00:54
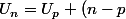r)
jusque là ça va??
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 01:03
par viina » 31 Déc 2008, 01:03
Billball a écrit: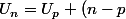r)
jusque là ça va??
oui jusque là ça va..
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 31 Déc 2008, 01:10
par Clembou » 31 Déc 2008, 01:10
viina a écrit:oui jusque là ça va..
Dans
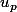
,

est un rang quelconque. Dans ton énoncé, tu connais quel terme de la suite ? Que vaut

? Ainsi après tu pourras remplacer la valeur de

dans la formule que te propose Billball et tu auras enfin la réponse à ta question...
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 01:22
par viina » 31 Déc 2008, 01:22
Clembou a écrit:Dans
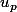
,

est un rang quelconque. Dans ton énoncé, tu connais quel terme de la suite ? Que vaut

? Ainsi après tu pourras remplacer la valeur de

dans la formule que te propose Billball et tu auras enfin la réponse à ta question...
je connais U1 qui est 14 000 et r -950 .
donc je remplace Up par 14 000 ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 01:25
par Billball » 31 Déc 2008, 01:25
remplace voir dans cette formule
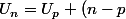r)
avec ce que tu connais soit U1 et r et aussi par ce que tu dois trouver U0
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 31 Déc 2008, 01:28
par Clembou » 31 Déc 2008, 01:28
viina a écrit:je connais U1 qui est 14 000 et r -950 .
donc je remplace Up par 14 000 ?
Donc si

, que vaut

???
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 01:31
par viina » 31 Déc 2008, 01:31
Clembou a écrit:Donc si

, que vaut

???
p c'est 1 .. ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 01:32
par Billball » 31 Déc 2008, 01:32
t'as tout compris, pu qu'à remplacer!
-
viina
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Déc 2008, 16:03
-
 par viina » 31 Déc 2008, 01:36
par viina » 31 Déc 2008, 01:36
Billball a écrit:t'as tout compris, pu qu'à remplacer!
donc
Un = U1 + (n-1) r
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 31 Déc 2008, 01:37
par Billball » 31 Déc 2008, 01:37
viina a écrit:donc
Un = U1 + (n-1) r
exprime en fonction de Uo et U1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
,
est un rang quelconque. Dans ton énoncé, tu connais quel terme de la suite ? Que vaut
? Ainsi après tu pourras remplacer la valeur de
dans la formule que te propose Billball et tu auras enfin la réponse à ta question...
