Complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tilmo
- Membre Naturel
- Messages: 24
- Enregistré le: 05 Nov 2008, 15:56
-
 par tilmo » 28 Déc 2008, 13:52
par tilmo » 28 Déc 2008, 13:52
bonjour!
on pose x=

montrer que:
1+2x+3x²+...+1992x^1991=

merci d'avance!
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 28 Déc 2008, 14:21
par acoustica » 28 Déc 2008, 14:21
tilmo a écrit:bonjour!
on pose x=

montrer que:
1+2x+3x²+...+1992x^1991=

merci d'avance!
Soit f(x)=x+x^2+...+x^1992=

f'(x)=1+2x+3x²+...+1992x^1991
Tu devrais t'en tirer en calculant f'(x) avec cette expression:
=x* \frac{x^1992-1}{x-1})
, ça devrais marcher je pense?
-
tilmo
- Membre Naturel
- Messages: 24
- Enregistré le: 05 Nov 2008, 15:56
-
 par tilmo » 28 Déc 2008, 14:41
par tilmo » 28 Déc 2008, 14:41
oui je sais le probleme c'est quand j fais la derivée de 1-x^1993/1-x ca ne m donne pas ce que je veux!
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 28 Déc 2008, 14:46
par acoustica » 28 Déc 2008, 14:46
tilmo a écrit:oui je sais le probleme c'est quand j fais la derivée de 1-x^1993/1-x ca ne m donne pas ce que je veux!
Ah? Je ne vois pas 36000 façons de faire, c'est vrai que c'est un peu calculatoire.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 28 Déc 2008, 15:21
par XENSECP » 28 Déc 2008, 15:21
tilmo a écrit:oui je sais le probleme c'est quand j fais la derivée de 1-x^1993/1-x ca ne m donne pas ce que je veux!
Donne nous la dérivée que tu trouves (détaille)
-
tilmo
- Membre Naturel
- Messages: 24
- Enregistré le: 05 Nov 2008, 15:56
-
 par tilmo » 28 Déc 2008, 16:48
par tilmo » 28 Déc 2008, 16:48
j'obtiens (1993x^1992(1-x)-(1-x^1993))/(1-x)² je trouve aussi que x^1992=1
je sais qu'on peut factoriser par 1-x.
est ce que 1-x^n=(1-x)(1+x+x²+...+x^(n-1))??
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 28 Déc 2008, 16:58
par XENSECP » 28 Déc 2008, 16:58
-(x^{1993}-1)}{(x-1)^{2}} = \frac{1992 x^{1993} - 1993 x^{1992} + 1}{(x-1)^{2}} = \frac{(x-1)(1992 x^{1992} - x^{1991} - x^{1990} - ... - x - 1)}{(x-1)^{2}} = \frac{(1992 x^{1992} - x^{1991} - x^{1990} - ... - x - 1)}{x-1} = \frac{(1992 x^{1992} - \sum_{k=1}^{1991} (x^{k})}{x-1})
Or tu sais que :
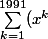} = \frac{x^{1992}-1}{x-1})
Je te laisse finir ?
-
jomanaomar
- Membre Naturel
- Messages: 44
- Enregistré le: 05 Juil 2008, 08:57
-
 par jomanaomar » 28 Déc 2008, 22:34
par jomanaomar » 28 Déc 2008, 22:34
Bonsoir tout monde,
on a f(x)=

=x*

La somme cherchée est donc
}{dx}= \frac{(x-1)(1993x^1992-1)-x^1993+x}{(x-1)^2})
on a

La somme =
(1993-1)-x+x}{(x-1)^2}= \frac{1992(x-1)}{(x-1)^2})
=

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités