Dm de noel casse tete !!
24 messages
- Page 1 sur 2 - 1, 2
dm de noel casse tete !!
salut a tous
j'ai des petits soucis pour un dm de noel et si vous pouvez y jeter un coup d'oeil svp merciiiii
voila le lien
http://img72.imageshack.us/img72/7751/numrisation0001ah0.jpg
pour l'exercice 1
je bloque a partir de la 1c) je ne comprends pas du tout comment y faut faire montrer que T°R....
pour l'exercice 2
1)a) j'ai dit que c'etait la somme d'une suite de n+1 terme consecutif... c'est bon?
b) j'ai donc trouvé z' = 1 + e^...+e^...
en deduire que la valeur de S alors la j'y arrive pas
besoin d'aide merci
merci
j'ai des petits soucis pour un dm de noel et si vous pouvez y jeter un coup d'oeil svp merciiiii
voila le lien
http://img72.imageshack.us/img72/7751/numrisation0001ah0.jpg
pour l'exercice 1
je bloque a partir de la 1c) je ne comprends pas du tout comment y faut faire montrer que T°R....
pour l'exercice 2
1)a) j'ai dit que c'etait la somme d'une suite de n+1 terme consecutif... c'est bon?
b) j'ai donc trouvé z' = 1 + e^...+e^...
en deduire que la valeur de S alors la j'y arrive pas
besoin d'aide merci
merci
sarah11 a écrit:http://img72.imageshack.us/img72/7751/numrisation0001ah0.jpg
Pfff t'aurais pu faire au-moins l'effort de scanner ton document dans le bon sens (ou alors c'est mon écran qui est à l'envers) :mur:
sarah11 a écrit:oops dsl :triste: je peux faire quelque chose?
voila pardon
http://img184.imageshack.us/my.php?image=numrisation0001ah0nv2.jpg
a l'endroit
Ensuite, pour la 2e question, il suffit comme l'énoncé l'indique d'adapter.
T:
R:
R o T: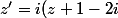 = iz + i + 2)
Il te suffit de trouver le point invariant désormais: tu sais de part la forme de ta transfo que c'est une rotation.
Pour R o T o T o R, ca équivaut, comme l'énoncé l'indique, a (R o T) o (T o R). Compose exactement comme ca, et simplifie. Comment sais-tu qu'une transfo est une symétrie centrale? En général, c'est de la forme ou T est complexe.
ou T est complexe.
T:
R:
R o T:
Il te suffit de trouver le point invariant désormais: tu sais de part la forme de ta transfo que c'est une rotation.
Pour R o T o T o R, ca équivaut, comme l'énoncé l'indique, a (R o T) o (T o R). Compose exactement comme ca, et simplifie. Comment sais-tu qu'une transfo est une symétrie centrale? En général, c'est de la forme
anima a écrit:Ensuite, pour la 2e question, il suffit comme l'énoncé l'indique d'adapter.
T:
R:
R o T:
Il te suffit de trouver le point invariant désormais: tu sais de part la forme de ta transfo que c'est une rotation.
Pour R o T o T o R, ca équivaut, comme l'énoncé l'indique, a (R o T) o (T o R). Compose exactement comme ca, et simplifie. Comment sais-tu qu'une transfo est une symétrie centrale? En général, c'est de la formeou T est complexe.
mais mois j'en suis a T°R
anima a écrit:Ah, tu n'arrives pas a établir le type de transformation?
Si je te dis que le coefficient multiplicatif de z est complexe...ca élimine pas mal de cas, non?
Ensuite, si le module de ce coefficient est un. Si tu es de niveau inférieur a celui du bac, il n'y a plus qu'un seul type possible.
oui j'en suis la
je me doute que c'est une rotation mais je c'est pas comment je fais pour prouver c'est la ou je bloque
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
