Dérivé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hgaet
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Mai 2008, 17:00
-
 par hgaet » 24 Déc 2008, 13:56
par hgaet » 24 Déc 2008, 13:56
Bonjour, j'ai un problème pour dérivé une fonction, elle est du type

. Dois-je dérivé
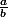
et prendre ce résultat pour dérivé le tout ?
Merci d'avance.
-
SimonB
 par SimonB » 24 Déc 2008, 14:33
par SimonB » 24 Déc 2008, 14:33
Dit comme ça, ça n'a aucun sens...
Que sont a, b et c dans ton "type" ? Des fonctions ? Des constantes ?
"Dériver" une fonction, c'est possible si au départ tu as une fonction (qui doit donc dépendre d'une variable...).
-
hgaet
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Mai 2008, 17:00
-
 par hgaet » 24 Déc 2008, 19:16
par hgaet » 24 Déc 2008, 19:16
La fonction c'est :
\frac{kx+1}{x} * e^x)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 24 Déc 2008, 19:23
par Euler911 » 24 Déc 2008, 19:23
Bonsoir.
Il te suffit d'appliquer la formule de la dérivée d'un produit:
soit f(x)=g(x)h(x)i(x)
f'(x)=g'(x)h(x)i(x)+g(x)h'(x)i(x)+g(x)h(x)i'(x)
dans ton cas, g(x)=kx+1
h(x)=1/x
i(x)=exp(x)
-
hgaet
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Mai 2008, 17:00
-
 par hgaet » 24 Déc 2008, 21:55
par hgaet » 24 Déc 2008, 21:55
D'accord, parce que cette formule on ne l'a pas encore vu, seulement avec un produit ou un quotient, de la forme

ou bien
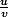
avec u et v 2 nombres réél.
Merci de votre aide et joyeux noel
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 25 Déc 2008, 01:28
par Huppasacee » 25 Déc 2008, 01:28
 = \frac{kx+1}{x} * e^x)
tu peux aussi écrire que c'est le produit u * v
avec u =

et v =

et tu appliques la formule de la dérivée d'un produit
pour u ' , c'est la dérivée d'un quotient
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 25 Déc 2008, 20:35
par oscar » 25 Déc 2008, 20:35
bonsoir f =[ ( kx+1)* e^x ]/ x est un quotient
On calcule f'(x) =
u = (kx+1) *e ^x=> u'=
v = x=> v' = 1
Puis (u/v)' = ( vu' +uv')/v²
f' (x) =...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
 . Dois-je dérivé
. Dois-je dérivé 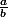 et prendre ce résultat pour dérivé le tout ?
et prendre ce résultat pour dérivé le tout ? 