Des nombres palindromes
22 messages
- Page 1 sur 2 - 1, 2
Des nombres palindromes
Démontre: Chaque entier naturel qui n'est pas divisible par 10 a une multiple qui est un nombre palindrome!
Malheureusement, j'ai aucune idée, comment on pourrait le démontrer. Est-ce que quelqu'un peut m'aider?
Merci beaucoup en avance!
Malheureusement, j'ai aucune idée, comment on pourrait le démontrer. Est-ce que quelqu'un peut m'aider?
Merci beaucoup en avance!
Mais le problème concerne des nombres qui ne sont pas "divisible" par 10. Cela ne veut pas dire que ces nombres sont premier avec 10!
En plus, est-ce que quelqu'un a une idée après quoi je doit chercher pour trouver le post que ThSQ cite? Je suis trop bête... :marteau:
À propos: merci pour votres réponses!
En plus, est-ce que quelqu'un a une idée après quoi je doit chercher pour trouver le post que ThSQ cite? Je suis trop bête... :marteau:
À propos: merci pour votres réponses!
Salut,
On considère la suite suivante modulo :
: 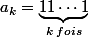 ,
, 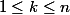
On dispose de restes : 0, 1, ..., n - 1. Si 0 est présent, alors c'est fini. Sinon, d'après le principe des tiroirs, il existe deux nombres
restes : 0, 1, ..., n - 1. Si 0 est présent, alors c'est fini. Sinon, d'après le principe des tiroirs, il existe deux nombres  et
et  ,
,  , qui ont le même reste modulo
, qui ont le même reste modulo  , c'est-à-dire :
, c'est-à-dire :



 \equiv 0 [n])
Comme est premier avec
est premier avec  par hypothèse, alors
par hypothèse, alors  d'après le théorème de Gauss. Le nombre
d'après le théorème de Gauss. Le nombre  est donc le multiple de
est donc le multiple de  recherché.
recherché.
raog a écrit:Démontre: Chaque entier naturel qui n'est pas divisible par 10 a une multiple qui est un nombre palindrome!!
On considère la suite suivante modulo
On dispose de
Comme
Zweig a écrit:Salut,
On considère la suite suivante modulo:
,
On dispose derestes : 0, 1, ..., n - 1. Si 0 est présent, alors c'est fini. Sinon, d'après le principe des tiroirs, il existe deux nombres
et
,
, qui ont le même reste modulo
, c'est-à-dire :


Commeest premier avec
par hypothèse, alors
d'après le théorème de Gauss. Le nombre
est donc le multiple de
recherché.
Et donc, 128 en exemple, ça fait quoi ?
La démonstration de Zweig inclut seulement les nombres premier avec 10. Bien sûr, tous les nombres qui sont divisible par deux n'ont pas un multiple qui ne comporte que des "1", car aucun multiple d'un nombre divisible par deux est impair!
Alors, la démonstration est un premier pas, mais il faut le montre pour les entiers divisible par 2 et les entiers divisible par 5 maintenant.
Évidemment:
128 * 33 = 4224
128 * 66 = 8448
128 * 318 = 40704
128 * 333 = 42624
128 * 348 = 44544
128 * 363 = 46464
128 * 378 = 48384
128 * 3168 = 405504
128 * 3333 = 426624
128 * 3498 = 447744
128 * 3663 = 468864
128 * 3828 = 489984
et autre exemple:
125 * 417 = 52125
125 * 421 = 52625
125 * 459 = 57375
125 * 463 = 57875
Alors, la démonstration est un premier pas, mais il faut le montre pour les entiers divisible par 2 et les entiers divisible par 5 maintenant.
Évidemment:
128 * 33 = 4224
128 * 66 = 8448
128 * 318 = 40704
128 * 333 = 42624
128 * 348 = 44544
128 * 363 = 46464
128 * 378 = 48384
128 * 3168 = 405504
128 * 3333 = 426624
128 * 3498 = 447744
128 * 3663 = 468864
128 * 3828 = 489984
et autre exemple:
125 * 417 = 52125
125 * 421 = 52625
125 * 459 = 57375
125 * 463 = 57875
raog a écrit:La démonstration de Zweig inclut seulement les nombres premier avec 10. Bien sûr, tous les nombres qui sont divisible par deux n'ont pas un multiple qui ne comporte que des "1", car aucun multiple d'un nombre divisible par deux est impair!
Alors, la démonstration est un premier pas, mais il faut le montre pour les entiers divisible par 2 et les entiers divisible par 5 maintenant.
Évidemment:
128 * 33 = 4224
128 * 66 = 8448
128 * 318 = 40704
128 * 333 = 42624
128 * 348 = 44544
128 * 363 = 46464
128 * 378 = 48384
128 * 3168 = 405504
128 * 3333 = 426624
128 * 3498 = 447744
128 * 3663 = 468864
128 * 3828 = 489984
et autre exemple:
125 * 417 = 52125
125 * 421 = 52625
125 * 459 = 57375
125 * 463 = 57875
Ben oui, y a plus qu'à.. :ptdr:
On prend un nombre n ni divisible par 10 ni premier avec 10.
n s'écrit m*p avec m premier avec 10, et p = 2^k ou 5^k.
On commence d'abord par trouver 2 entiers a et b tels que a*m = 10^b-1,
et on se ramène à étudier le cas de a*n = (a*m)*p = (10^b-1)*p.
Et quitte à devoir augmenter a et b, on peut supposer b > 2k.
Ensuite, on note que 10^k est un multiple de p, et donc (10^k-p)+10^k*("p mod 10^k en renversant les chiffres") aussi, donc il s'écrit p*q.
Et alors q*(p*(10^b-1)) est un palindrome.
Par exemple, en ayant b=13 et p = 2^4 = 16, on a que
3813124 * 16 = 61009984, et donc
3813124 * (16*(10^b-1)) = 61009984 * (10^b-1) = 610099839999938990016.
n s'écrit m*p avec m premier avec 10, et p = 2^k ou 5^k.
On commence d'abord par trouver 2 entiers a et b tels que a*m = 10^b-1,
et on se ramène à étudier le cas de a*n = (a*m)*p = (10^b-1)*p.
Et quitte à devoir augmenter a et b, on peut supposer b > 2k.
Ensuite, on note que 10^k est un multiple de p, et donc (10^k-p)+10^k*("p mod 10^k en renversant les chiffres") aussi, donc il s'écrit p*q.
Et alors q*(p*(10^b-1)) est un palindrome.
Par exemple, en ayant b=13 et p = 2^4 = 16, on a que
3813124 * 16 = 61009984, et donc
3813124 * (16*(10^b-1)) = 61009984 * (10^b-1) = 610099839999938990016.
Doraki a écrit:On prend un nombre n ni divisible par 10 ni premier avec 10.
(...)
J'ai beau réfléchir (remarque sérieuse..) je ne comprends pas pourquoi on fait l'assertion "ni premier avec 10". Est-ce que le fait qu'un nombre ne soit pas divisible par 10 n'exclut pas d'office le fait qu'il soit premier avec 10 ?
Je n'ai pas pris le temps de comprendre la preuve, je ne sais pas si cette assertion est nécessaire pour poser une hypothèse, ou si la répétition a été faite par inadvertance. Merci
A+
Doraki a écrit:Par exemple, en ayant b=13 et p = 2^4 = 16, on a que
3813124 * 16 = 61009984, et donc
3813124 * (16*(10^b-1)) = 61009984 * (10^b-1) = 610099839999938990016.
J'ai une question: Où est-ce que se trouve n dans cet exemple? Evidemment, q = 3813124, mais comment détermines-tu q?
Est-ce que c'est correcte que 10^k - p + 10^k * ("p mod 10^k en renversant les chiffres") = q? p mod 10^k est toujours p, n'est-ce pas?
Par exemple: 2^5 mod 10^5 = 2^5, car 0*10^5 + 2^5 = 2^5
euh ouais "p mod k en renversant les chiffres" c'est pas très bien dit.
Je veux dire qu'il faut prendre p en complétant à gauche avec autant de 0 qu'il faut pour avoir k chiffres, et puis renverser les chiffres.
Dans l'exemple, p c'est 16.
k=4 donc il me faut 4 chiffres : 0016
Je retourne : 6100
Maintenant, (10^k-p)+10^k*6100 ça fait 61009984, et c'est un multiple de 16 :
10^k = 5^k*2^k = 5^k*p, donc
(10^k-p)+10^k*6100 = p*(5^k-1+5^k*6100) = p*3813124.
Et dans l'exemple, n c'est n'importe quel diviseur de 16*(10^b-1).
Je veux dire qu'il faut prendre p en complétant à gauche avec autant de 0 qu'il faut pour avoir k chiffres, et puis renverser les chiffres.
Dans l'exemple, p c'est 16.
k=4 donc il me faut 4 chiffres : 0016
Je retourne : 6100
Maintenant, (10^k-p)+10^k*6100 ça fait 61009984, et c'est un multiple de 16 :
10^k = 5^k*2^k = 5^k*p, donc
(10^k-p)+10^k*6100 = p*(5^k-1+5^k*6100) = p*3813124.
Et dans l'exemple, n c'est n'importe quel diviseur de 16*(10^b-1).
Tout cela est vraiment intéressant, mais il nous faut une justification.
En premier, nous avons montré qu'il y a 2 entiers a et b tels que a*m = 10^b - 1. C'est clair, parce qu'il y a un multiple de m qui ne comporte que des 1. Et donc il y a aussi un multiple qui ne comporte que des 9.
Mais pourquoi peut-on dire qu'il est possible de augmenter a et b tels que b > 2k? Nous ne savons pas s'il y a plusieurs entiers a et b tels que a*m = 10^b - 1!
q*(p*(10^b-1)) est un palindrome. Ben, mais c'est plutôt comme un miracle. Je ne peut pas trouver une raison!
En tout cas, merci beaucoup pour la réponse! C'est déjà très utile :)
En premier, nous avons montré qu'il y a 2 entiers a et b tels que a*m = 10^b - 1. C'est clair, parce qu'il y a un multiple de m qui ne comporte que des 1. Et donc il y a aussi un multiple qui ne comporte que des 9.
Mais pourquoi peut-on dire qu'il est possible de augmenter a et b tels que b > 2k? Nous ne savons pas s'il y a plusieurs entiers a et b tels que a*m = 10^b - 1!
q*(p*(10^b-1)) est un palindrome. Ben, mais c'est plutôt comme un miracle. Je ne peut pas trouver une raison!
En tout cas, merci beaucoup pour la réponse! C'est déjà très utile :)
Pour pouvoir augmenter b, suffit de voir que
(10^b-1) * (10^b+1) = 10^(2b)-1 : avec ça tu passes de b à 2b.
Et que q*n est un palindrome, ben q a été choisi vraiment exprès pour faire apparaître les bons chiffres aux bons endroits... mais c'est pas marrant à vouloir vraiment démontrer (c'est ça l'ennui avec les problèmes sur les palindromes)
(10^b-1) * (10^b+1) = 10^(2b)-1 : avec ça tu passes de b à 2b.
Et que q*n est un palindrome, ben q a été choisi vraiment exprès pour faire apparaître les bons chiffres aux bons endroits... mais c'est pas marrant à vouloir vraiment démontrer (c'est ça l'ennui avec les problèmes sur les palindromes)
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
