DM sur les complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 22 Déc 2008, 10:55
par pspin » 22 Déc 2008, 10:55
bonjour, c'est mon premier post sur ce forum donc j'essaierai d'être le plus clair possible^^
donc voilà j'ai un DM pourtant sur les nombres comples et les racines nièmes a faire.
je bloque sur cette question:
soit l'équation
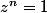
avec n entier supérieur ou egal a 1. on pose
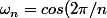+i*sin(2\pi/n)=exp(2i\pi/n))
il faut justifier que l'ensemble
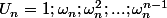
représente l'ensemble des solutions de l'équation
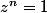
merci d'avance pour vos réponses
-
snakebirds
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Nov 2006, 21:36
-
 par snakebirds » 22 Déc 2008, 11:55
par snakebirds » 22 Déc 2008, 11:55
Z^n=1 on écrit Z sous forme exponentielle:
|Z|^n*exp(i*n*téta)=1 avec téta l'argument de Z
ssi:
|z|^n=1
n*téta=2*k*pi (k appartenant aux relatifs) car exp(2ikpi)=1
ssi:
|Z|=1 car |Z| supérieur à zéro
téta=(2*k*pi)/n
Les solution sont Un={exp(2*i*k*pi/n); k appartenant aux relatifs}
Mais comme la forme exponentielle complexe est 2pi périodique
Un={exp(2*i*k*pi/n); k appartenant à [|0;n-1|]}
donc Un=Wn^0;Wn;...;Wn^n-1
avec Wn^0=1.
Je ne sais pas si cette réponse (et cette question d'ailleurs) est du niveau lycée.
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 22 Déc 2008, 19:46
par pspin » 22 Déc 2008, 19:46
Merci de ton aide, et oui je me demande aussi de quel niveau est ce DM.
mais ce qui me fait le plus peur c'est que ce n'est que la première question...
donc attendez vous a me revoir xD
mais merci encore de ton aide précieuse^^
-
snakebirds
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Nov 2006, 21:36
-
 par snakebirds » 23 Déc 2008, 01:40
par snakebirds » 23 Déc 2008, 01:40
Bin à vrai dire le raisonnement est faisable en terminale mais je n'aurais pas su faire l'exercice sans l'usage de certaines notations que je pense n'avoir pas connu en terminale.
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 23 Déc 2008, 08:45
par pspin » 23 Déc 2008, 08:45
si c'est juste les notations, il n'y a aucun problème, on les a toutes vues.
mais c'est vrai que je n'avait pas pensé a écrire comme ça...
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 23 Déc 2008, 11:01
par pspin » 23 Déc 2008, 11:01
désolé pour le double post, mais il faut utiliser la formule:
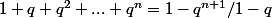
pour montrer quela somme des éléments de

est nulle.
je pose
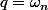
mais ça ne peut pas marcher car le dénominateur serait a ce moment nul, ce qui est impossible...
merci d'avance pour votre aide et votre réflexion
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 23 Déc 2008, 17:07
par pspin » 23 Déc 2008, 17:07
petit UP ^^
-
snakebirds
- Membre Naturel
- Messages: 38
- Enregistré le: 09 Nov 2006, 21:36
-
 par snakebirds » 23 Déc 2008, 17:12
par snakebirds » 23 Déc 2008, 17:12
Tu différencie le cas ou n=1 et n>=2,
Pour le cas ou n=1, U1=Wn^0 donc la somme des éléments de U1 valent Wn^0=1.
Pour le cas ou n>=2, somme=1-Wn^n/(1-Wn)=(1-exp(2ipi/n)^n)/(1-Wn)=1-exp(2ipi)/(1-Wn)=1-1/(1-Wn)=0.
Au fait pour ma réponse précédente j'ai écrit wo, w1,... c'est en fait Wn^0,Wn^1,Wn^2....Wn^n-1
-
pspin
- Messages: 6
- Enregistré le: 22 Déc 2008, 10:31
-
 par pspin » 23 Déc 2008, 18:13
par pspin » 23 Déc 2008, 18:13
ok merci beaucoup, pour la question précédente je m'en suis douté^^
bon je vais peut-être essayer de m'en sortir tout seul maitenant...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités