Questions sur la compacité

[seriousme]

Bonjour,

quelques questions sur la notion de compacité en topologie :

1) En quoi cette caractérisation est-elle importante ?
Auriez vous des exemples de propriétés de certaines partie d'un espace valides uniquement grâce à la compacité ?

2) Connaissez vous une caractérisation plus "opérationnelle", c'est à dire plus facilement utilisable dans le cadre de la mise en évidence de la présence ou l'absence de cette propriété, que celle par le recouvrement fini par des ouverts ?

3) Auriez vous des exemples de parties compactes et non compactes de en particuliers ?

4) Tout espace fini séparé est compact : est-ce le cas si l'espace est fini mais n'est pas séparé ?
Auriez vous des contre-exemples ?

Merci d'avance.

[ThSQ]

1) elle est très importante car c'est un invariant topologique (= conservée par homéomorphisme), que ça permet de donner plein de résultats (fonctions continues, ....) et qu'elle est bien élévée (elle passe au produit cartésien, au quotient, ...)

2) dans un espace métrique c'est équivalent à l'existence d'une suite extraite convergente pour toute suite (séquentiellement compacte).
Il y a d'autre caractérisations dans les métriques style précompact + complet. ,...
De manière générale, séquentiellement compacte et compacte sont deux notions séparées.

3) dans (IR, |.|), compact = fermé + borné

4) en français compact = séparé + recouvrement blah blah
C'est différent en anglais où compact = recouvrement blah blah (= quasi-compact à la sauce Bourbaki) sans supposition de séparation.

[ShakkaChan]

1) oui la compacité est très importante tu verra dans la suite que beaucoup de théorème ou de résultat sont du a la présence de compacité
par exemple beaucoup de résultat d'existence de solution des EDP utilise la compacité.
2) un espace est compact si de toute suite de l'espace tu peut extraire une sous suite qui converge dans l'espace
c'est plutot ca qu'on utilise au debut
3) tout les fermé borné de R sont compact et donc les ouvert ne le sont pas
en dimension superieur les compact sont fermé borné mais ce n'est pas suffisant
4) pour les métrique tout métrique étant separé un espace fini est compact
dans le cas des espace topologique je sais pas trop

[R.C.]

Pour la 4), sur un espace fini, tu n'as qu'un nombre fini d'ouverts, donc si tu est anglais, un espace fini est toujours compact, mais si tu es français il faut qu'il soit séparé par def. Si tu veux une topologie non séparée, je te conseille de prendre le moins d'ouverts possible.

[jeancam]

tous les fermé borné de R sont compact et donc les ouvert ne le sont pas

sans vouloir chipoter je dirais "et" pour "donc" ou "seul" pour "tous" (je dirais bien que ces trois derniers mots feraient un bon titre si je ne craignais d etre déplacé dans le rubrique poesie qui n existe pas)

[jeancam]

je post quelque chose dans enigme qui a un rapport avec des compacts finis j aimerais bien ecrire en bleu souligné un "ici" mais je sais pas comment on fait. si quelqu un peut m expliquer...

[seriousme]

Tout d'abord merci de toutes vos réponses très instructives.

Cependant si vous aviez une explication plus "sémantique" du concept sans utiliser des caractérisations trop formelles comme les suites convergentes :
- Que signifie t'il ?
- A quel concept non mathématique peut il être comparé ?
De même que la notion de densité topologique peut être comparée à celle de densité de matière en physique.

Pour faire un lien vers l'autre topic :


Merci.

[jeancam]

Tout d'abord merci de toutes vos réponses très instructives.

Cependant si vous aviez une explication plus "sémantique" du concept sans utiliser des caractérisations trop formelles comme les suites convergentes :
- Que signifie t'il ?
- A quel concept non mathématique peut il être comparé ?
De même que la notion de densité topologique peut être comparée à celle de densité de matière en physique.

Pour faire un lien vers l'autre topic :


Merci.

je pense que "compact" dit bien ce que c est
les compacts de l espace tridimentionnel sont les fermés bornés c est à dire sans rentrer dans des considerations quantiques ou je n y connais rien les objets tels qu on les conçoit: on imagine mal un paquet de clope "sans le bord"...mais çà n engage que moi...

sinon si tu reflechis un tout petit peu à la définition (qui a l air peut etre un peu bizare avant reflection) tu te rendra compte qu elle est en fait assez "naturelle"...

ps
je suis mine de rien assez satisfait de mon interpretation sémanticopsycologicophysique de la compacité...notion du coup on ne peut plus naturelle pour notre esprit si on voit les choses sous cet angle

j aurais bien continué cette discution au café
peut etre qu on pourra faire çà dans la nouvelle version
ou c est peut etre possible de déplacer juste quelque posts ou d avoir la meme discution dans deux categories
en tout cas les LIENS entre les posts me paraissent une bonne idée...

[seriousme]

Merci de votre illustration plus informelle.

Par exemple est-ce que l'ensemble des rationnels est compact dans ?
A priori non car il est possible de construire un recouvrement infini duquel il n'est pas possible d'extraire un recouvrement fini : en prenant les intervalles ouverts avec quelquonque par exemple.

En revanche l'ensemble des rationnels d'un intervalle est compact car aussi petit qu'est le nombre d'ouverts recouvrant les rationnels peut être réduit à un recouvrement fini.

Est-ce cela ?

[abcd22]

Bonsoir,
C'est écrit au-dessus « dans R (et dans R^n aussi), compact = fermé + borné ».

[seriousme]

Oui mais sans utiliser d'autres propriétés que les axiomes définissant la compacité pour une partie d'un espace, ces affirmations peuvent elles être confirmées/infirmées ?

[R.C.]

Ben si tu prend Q intersecté avec [0,1], regarde le recouvrement ouvert suivant : fixe i dans [0,1] irrationnel, et prends la suite r_n = i-i/n (r_1=0) qui converge vers i. Alors je prend ]i,1] et ]r_n-(i-r_n)/2,r_n+(i-r_n)/2[ et tu n'arrivera pas à en tirer un sous recouvrement fini (tu peux faire un dessin pour t'aider).

[seriousme]

Merci beaucoup de votre exemple.

Donc "l'astuce" de l'exemple est que les ouverts sont décentrés les uns par rapport aux autres et donc il est impossible d'extraire un recouvrement fini de ce recouvrement ?

Sinon i n'est t'il pas plutôt rationnel ?

[R.C.]

Sinon i n'est t'il pas plutôt rationnel ?

Ah ben non, justement, il faut le prendre irrationnel parce que en fait c'est le seul point de [0,1] qui n'est pas recouvert.

[seriousme]

Ah oui en effet.

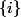
Donc si on ajoute au recouvrement il recouvre ?
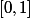
Dans ce cas quel sous-recouvrement fini de ce recouvrement est-il possible de trouver qui recouvre ?

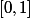
[R.C.]

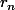
En fait n'est pas un ouvert, mais si on ajoute un ouvert contenant i, alors il va contenir un bon paquet des (tous ceux pour mettons). Alors le sous-recouvrement ca doit être qqchose comme et les pour et l'ouvert contenant i.

[seriousme]

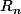
En effet et dans ce cas ce recouvrement sera fini car, aussi petit que soit , contiendra une infinité de terme de après .

Cet exemple est excellent car il illustre bien sur un même ensemble la compacité et la non compacité.

Merci encore.

[seriousme]

Pour démontrer que l'ensemble E des rationnels de [0, 1] n'est pas compact mais cette fois en utilisant la caractérisation de Bolzano-Weierstrass : est-il possible de dire que tout irrationnel i de [0, 1] est la limite de la suite dont le nième terme est constitué des n premières décimales de i ?

Par exemple pour :


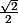
Cette suite a pour seule valeur d'adhérence i et donc n'en a pas dans E, donc la suite ne converge pas dans E, donc E n'est pas compact.

Est-ce un argument valide ?

Merci.

[SimonB]

Oui, c'est valide !

[seriousme]

Merci de la confirmation.

Une question encore :
Est-ce que tout ouvert est non compact ?

Dans oui car les seuls compacts sont les fermés et bornés, mais ce résultat se généralise t'il ?

Si ce n'est pas le cas auriez vous des exemples d'ouverts compacts ?

Merci.