Hyperplan

[jeremy58]

Bonjour,
je dois trouver un contre-exemple pour la proposition suivante car il me semble que c'est faux.
Si U est un sous-ensemble fermé non vide de et U possede un hyperplan d'appui en tout point de sa frontiere, alors U est convexe.
Sachant qu 'un hyperplan d'appui est :
H est un hyperplan d'appui à un ensemble convexe C de en un point x C si x et C inclu dans .
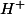
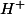
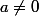
ou ={} avec et .
Merci d'avance pour votre aide

[R.C.]

Bonjour,
Si U n'est pas connexe, tu peux trouver un contre exemple assez facilement. Par contre, si U est connexe, ça me parait plutot vrai.
Edit: bon ok en fait j'ai l'impression que c'est vrai si c'est d'intérieur non vide (voir post suivant)...

[ThSQ]

contre-exemple

Les contrex ne manquent pas !

- deux points quelconques distincts (tout hyperplan qui passe par un des points est d'appui !)
- un cercle
- le graphe d'une fonction continue convexe ou concave
- plus généralement un convexe fermé d'intérieur non vide auquel on enlève l'intérieur


Edit : d'ailleurs on peut se demander quelles conditions suffisantes on peut ajouter pour que cela devienne vrai.

Par exemple pour continuer le dernier exemple : et si on ajoute la condition que le bidule est d'intérieur non vide ? :ruse:

[jeremy58]

Je vous remercie beaucoup, vous m'avez beaucoup aidé.
Encore merci

[ThSQ]

De rien,

si on ajoute la condition que le bidule est d'intérieur non vide ? :ruse:

J'm'réponds, comme d'hab mes exos font un bide :ptdr:

Exo : mq que ça marche :id:


Si U est un sous-ensemble fermé non vide de , si U est d'intérieur non vide et si U possède un hyperplan d'appui en tout point de sa frontiere, alors U est convexe.