Voilà j'suis dans le cacul d'une Value At Risk, pour trois titres dans un portefeuille, ces trois titres étant corrélés entre eux.
Donc j'aimerais savoir si quelqu'un connait la formule pour calculer une variance pour trois variables non independantes?
Var (A+B+C) = ?
Dans ce cas les trois titres sont equipondérés.
Mais j'aimerais savoir comment faire lorsqu'on veut mettre par exemple 50% du titre A, 30% du titre B, et 20% du titre C ?
Merci beaucoup !
Variance pondérée de plus de deux variables
3 messages
- Page 1 sur 1
bonjour,
De manière générale tu as la formule suivante
=\displaystyle\sum_{i=1}^{i=n}\sum_{j=1}^{j=n}p_ip_jCov(X_i,X_j))
avec les ponderations des variables (leur somme vaut 1)
les ponderations des variables (leur somme vaut 1)
Cette formulE semble assez barbare, mais au final pas mal de choses se simplifient
1°) Pour les termes avec i=j,=Var(X_i))
2°) Par symetrie sur les indices i et j tu as des termes qui apparaissent deux fois
La formule peut donc se simplifié un peu et se rééecrire comme
=\left(\displaystyle\sum_{i=1}^{i=n}(p_i^2Var(X_i)\right)+2\left(\displaystyle\sum_{i=1}^{i=n} \sum_{j>1}^{j=n}p_ip_jCov(X_i,X_j)\right))
Remarque avec cette écriture que si les variables sont indépendantes (i.e. covariance nulles) la variance de ta somme est la moyenne pondérée des variances.
Remarque également que en écriture matricielle, la variance de ta somme est donc donnée par le produit matriciel
=P^t.\Sigma.P)
ou P est le vecteur colonne des poids et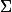 la matrice de variance covariance.
la matrice de variance covariance.
Pour finir, lorsque n=3 (ton cas) il y a donc au final 3 variances à calculer et 3 covariance.
En esperant avoir répondu à ta question.
(PS : Cette formule a un nom "formule de...", mais je ne le retrouve plus...si quelqu'un s'en souvient...)
De manière générale tu as la formule suivante
avec
Cette formulE semble assez barbare, mais au final pas mal de choses se simplifient
1°) Pour les termes avec i=j,
2°) Par symetrie sur les indices i et j tu as des termes qui apparaissent deux fois
La formule peut donc se simplifié un peu et se rééecrire comme
Remarque avec cette écriture que si les variables sont indépendantes (i.e. covariance nulles) la variance de ta somme est la moyenne pondérée des variances.
Remarque également que en écriture matricielle, la variance de ta somme est donc donnée par le produit matriciel
ou P est le vecteur colonne des poids et
Pour finir, lorsque n=3 (ton cas) il y a donc au final 3 variances à calculer et 3 covariance.
En esperant avoir répondu à ta question.
(PS : Cette formule a un nom "formule de...", mais je ne le retrouve plus...si quelqu'un s'en souvient...)
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
