Bonjour a tous,
apres longue reflexion il me semble qu'il ya une erreur dans mon enoncé et je vous donne raison ThSQ, il faut que

soit convexe.
Alors je reprend du depart, je sais et j'ai deja montrer que :
jeremy58 a écrit:\Omega Compact
f est strictement convexe

f est lipschitz de constante L
on etudie la methode du gradient projete avec
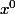
fixé,
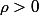
fixé

f(x^k)
-f(x^k)\leq (L-\frac{1}{\rho})||x^{k+1}-x^{k}||^2)
je dois montrer que :
il existe une valeur d'adherence s de la suite
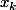

pour tout

Voila ce que j'ai fait, je voudrais votre avis,
f continue et

compact alors f admet au moins un minimum. De plus, f strictement convexe et

convexe alors f admet un unique minimum.
Comme
)
bornée, par Bolzano-Weierstrass, toute suite bornée admet au moins une valeur d'adherence. Donc il existe s tel que s valeur d'adherence de
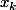
.

vient aussi de B-W.
Et pour l'inegalité,
Pour tout
 \leq f(s+\theta(x-s)))
Pour tout
)-f(s)}{\theta} \geq 0)
On fait tendre

Pour tout

.
Est-ce que j'ai le droit d'ecrire tout ca.
Merci d'avance pour votre aide
