Les complexes (argument)

[mamertin]

Bonjour, bonsoir ,

Donc voila voilou j'ai un probleme en ... math :we: étonnant?

Tout d'abord voici l'énoncé pour rentrer dans l'exercice:
Déterminer l'ensemble des points M d'affixe z tels que :

a) arg(z-2i)=pi/4
b)arg(z²-4)=arg(z+2)
c)arg(1/(z+2))=pi/2
d)arg(/z + i )=2pi/3 (/z = z barre)

Voila je ne vous demande pas de me donner la réponse toute prete mais juste une méthode, une explication pour que je puisse faire cette exercice
merci d'avance

[uztop]

Salut,

est ce que tu connais un nombre dont le module vaut ?
Ensuite, si deux complexes ont le même module, qu'est ce que tu peux dire ?

[Florélianne]

Bonjour,
Déterminer l'ensemble des points M d'affixe z tels que :
il faut utiliser les deux écritures possibles pour trouver z
a) arg(z-2i)=pi/4
donc z-2i = lz-2ilcos(pi/4)
écrisz = x+iy calcule z-1 puis lz-il
tu obtiens deux écritures différentes de z-i
à toi de déterminer x et y
puis les "lieux géométriques" des points
b)arg(z²-4)=arg(z+2)
c)arg(1/(z+2))=pi/2
d)arg(/z + i )=2pi/3 (/z = z barre)
bon travail

[mamertin]

oki d'ac je me lance et je t'envoi ce que j'ai trouvé si ca ne te dérange pas :/

edit: pourquoi calculer z-1 et /z-i/?

[mamertin]

sinon je trouve z-1=x+iy-1
/z-i/=racine(x²+y²-2y+1)

[uztop]

Florélianne, je trouve que tu te compliques un peu la vie là.
On sait par exemple que 1+i a pour argument pi/4; qu'est ce qu'on peut dire de deux nombres qui ont le même argument ?

[mamertin]

Deux nombres qui ont le meme argument ont le meme module ?

[uztop]

non, est ce que tu sais ce que représentent géométriquement le module et l'argument ?

[mamertin]

le modules est la longueur et l'argument l'angle.

[uztop]

oui, donc si deux complexes ont le même angle, cela signifie qu'ils sont sur une même droite et donc qu'ils sont multiples l'un de l'autre. Est ce que tu es d'accord avec ça ?

[mamertin]

Oui je suis d'accord =)

[uztop]

Donc pour le a) , je pense que tu peux répondre à la question :)

[mamertin]

arg(z-2i)=pi/4
arg(1+i)=pi/4

/z-2i/=/1+i/
/x+iy-2i/=/1+i/
racine(x²+(y-2)²)=racine(2)
x²+y²-2y+4=2

Mais ensuite comment puis je faire?

[uztop]

non, le fait que les arguments soient égaux ne veut pas dire que le module est égal (au fait, si tu as clavier français, le | s'écrit avec Alt-Gr 6)
Par contre, on sait que
z-2i = k(1+i) : c'est ce qu'on a dit tout à l'heure, les deux complexes sont proportionnels parce qu'ils ont le même module.
Dis moi si tu n'as pas compris.

[mamertin]

Donc non je n'es pas compris pourquoi ils sont proportionnels et qu'elle est la marche a suivre ( le résultat doit bien etre y=...?)

[uztop]

ok, alors considérons un point M d'affixe z.
|z| représente la distance OM
arg(z) représente l'angle

Maintenant, si on a un deuxième point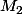 d'affixe 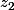tel que arg(z) = .
z et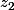 se trouvent sur la même droite: O, M et 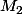sont alignés; les deux points ne sont différenciés que par le module qui est différent.
z = |z| arg(z)

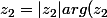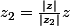Comme arg(z) = , on peut dire que et ils sont donc proportionnels (avec un coefficient de proportionnalité réel)

Sinon, non, on ne cherche pas un résultat de la forme y= ... ?, mais plutôt en z=

[mamertin]

Donc je te suis jusqu'a Z2=(|z|/|Z2|)z et puis meme on ne connait pas les module ...

Pour moi Z2= |Z2| arg(Z)

[uztop]

c'est juste pour dire qu'ils sont proportionnels |z|/|Z2| est le coefficient de proportionnalité mais peu importe à la limite.
On peut donc dire, dans le cas de ton exo que :
(z-2i) est proportionnel (avec un coeff de proportionnalité réel et positif) à 1+i

[mamertin]

Donc la je suis totalement d'accord mais comment cela nous mene t-il a l'ensemble des points M?

[uztop]

oui, de façon géométrique ça donne:
z-2i représente la demi-droite d'équation y=x qui commence en O avec un angle de 45 degrés.
Pour z, il faut ajouter 2i à cette droite, c'est à dire une translation d'un vecteur 2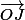 (je te conseille de faire un dessin pour voir un peu mieux) : au total on obtient donc une demi droite d'un angle de 45 degrés et qui démarre au point de coordonnées (0;2)