Homéomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Prison Break
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Nov 2006, 14:42
-
 par Prison Break » 12 Déc 2008, 17:40
par Prison Break » 12 Déc 2008, 17:40
Bonjour
Soit

----->
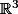
)
----->
)
.
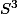
est l'hypersphère de
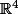
(
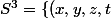 \in \R^4 , x^2+y^2+z^2+t^2=1\})
)

est le point nord de la sphère
)
la question est la suivante : montrer que

est un homéomorphisme de

vers
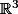
.
que je doit vérifier ou prouver pour qu'elle soit héomorphisme ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 12 Déc 2008, 17:52
par ThSQ » 12 Déc 2008, 17:52
Que c'est bien défini, continue et surtout que la réciproque est continue (un passage par le compactifié permet de sauter une étape pour les plus hardis ;))
-
Prison Break
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Nov 2006, 14:42
-
 par Prison Break » 12 Déc 2008, 18:00
par Prison Break » 12 Déc 2008, 18:00
merci ThSQ
Bon phi est bien défini et continue (évidente !)pour la réciproque mmmmm !et si je calcule (phi)^(-1) ! et voir si elle est continue
-
Prison Break
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Nov 2006, 14:42
-
 par Prison Break » 12 Déc 2008, 18:01
par Prison Break » 12 Déc 2008, 18:01
et il faut d'aobrd montrer qu'elle est bijective non ?
-
Prison Break
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Nov 2006, 14:42
-
 par Prison Break » 12 Déc 2008, 18:08
par Prison Break » 12 Déc 2008, 18:08
injectivité :phi(a)=phi(b) ===> a=b



et aprés ?????? :doh:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 12 Déc 2008, 18:18
par Doraki » 12 Déc 2008, 18:18
Calcule d'abord la réciproque.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités