Triangle isocele dans un cercle trigonometrique

par **Matthy** » 04 Jan 2006, 01:12

Bonjour a tous,
voila, j'ai un exercice a faire sur lequel je bloque, je signale que c'est un exercice de 1S. Voici l'enonce.

Sur un cercle trigonometrique, les points A et B sont reperes par pie/3 et 3pie/4.
Determiner les points M du cercle tels que le triangle ABM soit isocele.

Je me dis bien qu'il doit falloir utiliser des angles, mais je ne sais pas vraiment comment. Merci d'avance pour votre aide.

(EX 104 p298 dans Trans Math 1reS)

par **Chimerade** » 04 Jan 2006, 01:42

Calcule la distance entre deux points

et

du cercle trigonométrique repérés par les angles

et

. Tu peux le faire géométriquement ou analytiquement. Tu dois trouver :

Ainsi, pour le cas où tu cherches un point C (repéré par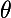

) tel que CA=CB, la condition "isocèle en C" se traduit par :

et cette équation se traduit par deux équations :

et

que tu n'as plus qu'à résoudre

Reste bien sûr les deux cas où AC=AB (isocèle en A) et où BC=BA (isocèle en B), mais c'est du même tabac...

par **Matthy** » 04 Jan 2006, 02:15

Merci pour ta reponse mais je ne comprends pas vraiment....

Comment trouves- tu les equations avec les sin?
Mais on ne peut pas tout simplement utiliser le fait que dans un triangle isocele les angles a la base on meme mesure? (je sais que ce n'est pas suffisant, mais cela ne peut-il pas etre un bon depart de recherche?)

par **Chimerade** » 04 Jan 2006, 03:40

Il faudrait que tu me dises ta classe pour que je sache comment t'aider !

La méthode que je te propose n'est pas la seule possible. Si tu veux raisonner par rapport aux angles à la base de ton triangle isocèle, pourquoi pas ? Mais cela me parait plus compliqué, au moins a priori !

par **Matthy** » 04 Jan 2006, 13:09

Matthy a écrit: c'est un exercice de 1S.

Disant cela je pensais que tu pourai comprendre que je suis en 1ereS. Car en fait tout ce que tu ma dit un peut plus haut c'est un peu du charabia pour moi....
Merci de ton aide, mais si tu vois une solution plus simple et de mon niveau n'esite pas a m'en faire part.

par **Chimerade** » 04 Jan 2006, 13:40

C'est parce que tu n'as pas compris ce que j'ai dit que je te croyais dans une classe moins élevée que 1ère S !
Je ne voudrais pas te décevoir, mais j'avais craint que tu fusses en troisième ou en seconde par exemple, où on aurait pu te demander ce genre de problème à résoudre géométriquement. Mais en première, première S qui plus est, ya pas photo ! Tu dois savoir que :

1- La longueur d'un segment allant d'un point

à un point

est :

2 - Un point du cercle trignonométrique repéré par l'angle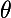

a pour coordonnées :

et

Par conséquent il est facile de calculer la distance entre deux points

et

, repérés respectivement par les angles

et

:

ce qui toutes simplifications faites donne :

En outre la résolution d'une équation du type sin(A)=sin(B) est tout-à-fait à ta portée.

Désolé ! Un élève de première doit comprendre tout cela...Mais, bon !

par **Matthy** » 04 Jan 2006, 13:51

Merci du detaille, maintenant, avec les explications je comprends mieu. C'est juste que sorti comme ca je ne comprenais pas comment tu l'avais trouve. Merci beaucoup.

par **mathos86** » 04 Jan 2006, 14:06

Il y a trois problèmes en 1, chacun des trois est très simple, il suffit de faire une figure différente pour chaque problème.

PB1: ABM isocèle en M
On a alors: M appartient à la médiatrice de [AB] qui a deux points d'intersection avec le cercle. Il te reste à trouver les angles qui repèrent ces deux points sur le cercle et à rédiger ta démonstration.

PB2: ABM isocèle en A
On a alors AM = AB donc M appartient au cercle de centre A et de rayon AB qui a deux points d'intersection avec le cercle trigonométrique, mais l'un de ces points est B qui ne convient pas. Il te reste à trouver l' angle qui repère l'autre point sur le cercle et à rédiger ta démonstration.

PB3: ABM isocèle en B
même chose que PB2; il faut refaire les calculs mais il est inutile de rédiger la démonstration.

par **mathos86** » 04 Jan 2006, 14:14

Les explications de Chimerade ne sont pas à la portée d'un (bon) élève de 1S et surtout ne présententent aucun intéret car elles ne reflètent pas le niveau de l'exercice.

par **bdupont** » 04 Jan 2006, 14:17

Salut Matthy,

Pour ceux qui sont allergiques à la trigo, on peut considérer I le milieu de AB et voir que si ABM est isocèle en M, alors I,O et M sont alignés.
I a pour coordonnées ((1+rac(2))/4, (rac(2)+rac(3))/4).

Pour trouver M(x,y) on résoud un système de 2 équations :
une première équation traduit le fait que OM et OI sont colinéaires (déterminant nul) et une seconde le fait que M est sur le cercle (x^2 +y^2 = 1)

Bien sûr ça manque singulièrement d'élégance mais on ne parle pas de trigo et on peut résoudre le problème dès la seconde. Il suffit de savoir ce qu'est un cercle trigonométrique et connaître les valeurs des sinus et cosinus de pi/3 et 3pi/4.

par **mathos86** » 04 Jan 2006, 14:28

Au risque de lasser, je maintiens que cet exercice porte sur le repérage polaire d'un point du plan et que passer par les coordonnées cartésiennes est une erreur.

par **rene38** » 04 Jan 2006, 14:43

Bonjour

Une autre approche :
Si ABM est isocèle en M alors M est le milieu d'un des arcs (AB).
Il est donc repéré par

ou

Si ABM est isocèle en A alors A est le milieu de l'arc (BM).
Il est donc repéré par

tel que

donc

Si ABM est isocèle en B alors B est le milieu de l'arc (AM).
Il est donc repéré par

tel que

donc

par **mathos86** » 04 Jan 2006, 14:50

Le milieu d'un arc n'étant pas défini, ces égalités doivent être justifiées autrement (bissectrices ou autres considérations sur les angles).

Triangle isocele dans un cercle trigonometrique

Triangle isocele dans un cercle trigonometrique

Simple

Pas d'accord

Thème: repérage polaire d'un point.

Bissectrices

Qui est en ligne