Exercice exponentielle

[sup3rman]

Bon j'ai un petit problème avec un exercice sur la fonction exponentielle,

f(x)= x - ( (e(x)-1) / (e(x)+1))

j'ai démontré qu'on pouvait l'écrire sous la forme

f(x)= (x-1) + ( (2) / (e(x)+1) )
f(x)= (x+1) - ( (2e(x)) / (e(x)+1) )

j'ai étudié les limites de f en + et - l'infini

et maintenant je doit démontrer que les droite d'équation d1 et d2 d'équation y=x+1 et y=x-1 sont asymptotes à C respectivement en - et en + l'infini.

j'ai penser à étudier la limite de f(x)-(ax+b) en +l'infini qui me permettrai de dire que c'est une asymptote oblique mais je n'y arrive pas, suis je bien parti ?

merci

[nuage]

Salut,

f(x)= (x-1) + ( (2) / (e(x)+1) )

Ce qui suffit pour l'étude de l'asymptote en :
quelle est la limite de ( (2) / (e(x)+1) ) en ?

Pour l'asymptote en calcule f(x)-(x+1).

[uztop]

bonsoir,

oui, plus précisément, pour étudier si y=x+1 est une asymptote oblique en - l'infini, il faut étudier f(x)-(x+1)

[sup3rman]

quelle est la limite de ( (2) / (e(x)+1) ) en ?

0 mais la limite de (x-1) va être + l'infini et il faut que la limite soit x-1 pour qu'elle soit asymptote ?

[nuage]

Un petit rappel de cours :
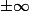
La droite d'équation est asymptote (oblique) à la courbe en si et seulement si

[sup3rman]

Ah sa marche aussi en -l'infini. J'ai réussi pour y=x-1
mais pour x+1
sa me donne lim 2e(x) / e(x)+1
j'ai essayé de factorisé par e(x) mais je bloque ensuite... faut-il la mettre sous une autre forme?

[sup3rman]

quelqu'un pourrait-il m'aider ? :we:

[Neirh]

bonsoir,
pas besoin de factoriser :
quelle est la limite de e(x) en - l'infini?

[sup3rman]

quelle est la limite de e(x) en - l'infini?

0, je pensais que sa menait à une forme indéterminée, donc lim = 0/1 = 0

donc y=x+1 est asymptote oblique à la courbe

[sup3rman]

si on prend la première forme de f(x), sa dérivé est bien
f'(x)= 1 - ( 2ex / (ex+1)² )
?

vu que sa dérivé est positive quand x>0, f(x) est donc croissante. ?