Bonjour!
J'ai quelques petits problèmes ac un exercice de Maths, sur les PGCD.
En fait on a a = 7n+20 et b = 2n+7.
Sachant que: 2n+20 = 3(2n+7)+(n-1)
et : 2n+7= 2(n-1)+9
Il faut en deduire que PGCD(a;b) = PGCD (n-1;9)
Donc si vous voyez quelle relation permet de dire ca, ej serais ravie d'avoir quelques tuyaux!
Merci d'avance!
Spé Maths - PGCD
6 messages
- Page 1 sur 1
Bonsoir :happy3:
=d\\PGCD(n-1;9)=D)
Essayons de montrer que D|d et d|D ce qui nous permettra de conclure que D=d :
1)
Comme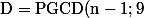) , par définition,
, par définition,  et D|9)
Ainsi D divise toute combinaison linéaire de ces deux nombres et en particulier :
-9) , ie D|b)
En utilisant ce dernier résultat, on peut encore écrire :
), ie D|a)
Finalement,
donc :
2)
d étant le PGCD de a et b, il divise de même toute combinaison linéaire de ces deux nombres.
Ainsi :
, ie d|(n-1))
Avec ce dernier résultat :
), soit d|9)
On a prouvé et d|9)
En on conclut :
3) Conclusion :
 et en en déduit comme prévu
et en en déduit comme prévu 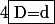
Essayons de montrer que D|d et d|D ce qui nous permettra de conclure que D=d :
1)
Comme
Ainsi D divise toute combinaison linéaire de ces deux nombres et en particulier :
En utilisant ce dernier résultat, on peut encore écrire :
Finalement,
donc :
2)
d étant le PGCD de a et b, il divise de même toute combinaison linéaire de ces deux nombres.
Ainsi :
Avec ce dernier résultat :
On a prouvé
En on conclut :
3) Conclusion :
Soit d un diviseur commun à n-1 et à 9 ; puisque 2n+7=2*(n-1)+9, d divise 2n+7. Tous les diviseurs communs à n-1 et à 9 divisent 2n+7 et n-1 !
Soit d' un diviseur commun à 2n+7 et à n-1. Comme 9=2n+7-2*(n-1), d' divise 9. Donc tous les diviseurs communs à 2n+7 et à n-1 divisent 9 et n-1.
Par conséquent la liste des diviseurs communs à 2n+7 et à n-1 est la même que la liste des diviseurs communs à 9 et à n-1. Le plus grand nombre de cette liste est donc à la fois PGCD(n-1;9) et PGCD(2n+7,n-1).
Tu n'as qu'a continuer :
Soit d un diviseur commun à 2n+7 et à n-1. Comme 7n+20 = 3(2n+7)+(n-1), d divise 7n+20,...
Soit d' un diviseur commun à 2n+7 et à n-1. Comme 9=2n+7-2*(n-1), d' divise 9. Donc tous les diviseurs communs à 2n+7 et à n-1 divisent 9 et n-1.
Par conséquent la liste des diviseurs communs à 2n+7 et à n-1 est la même que la liste des diviseurs communs à 9 et à n-1. Le plus grand nombre de cette liste est donc à la fois PGCD(n-1;9) et PGCD(2n+7,n-1).
Tu n'as qu'a continuer :
Soit d un diviseur commun à 2n+7 et à n-1. Comme 7n+20 = 3(2n+7)+(n-1), d divise 7n+20,...
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
