Aire A(x) d'un triangle

par **Swann** » 07 Déc 2008, 14:09

bonjour,
je n'arrive pas a repondre a cette question :

dans un repére orthonormal on considère le cercle (C) de centre 0 et de rayon 1. on note A le point de coordonnées (1,0) et A' le point de coordonnées (-1,0). Par un point H du segment [A,A'], distinct de A et de A', on mène la perpendiculaire (D) à la droite (A,A'). La droite (D) coupe le cercle (C) en M et M'. On note x l'abscisse de H dans le repère choisi.

1/ Calculer en fonction de x, l'aire A(x) du triangle AMM'.
2/ montrer que le triangle AMM' d'aire maximale est équilatéral.

Pour la première question, je sais que l'aire d'un triangle c'est [base x hauteur]/2
donc ici ça fait : MM' x AH / 2
mais je vois pas comment calculer ces deux longueurs...
pour AH j'ai les coordonnées de A(1,0) et de H(x,0) mais pour MM' j'ai rien :s...

merci de m'aider.

par **phryte** » 07 Déc 2008, 14:20

Bonjour.
A(x)=x*HM
HM est l'ordonnée du point d'abscisse x du cercle d'équation : x^2+y^2=1
.....

par **Swann** » 07 Déc 2008, 14:44

euh.. je comprends pas :$

par **phryte** » 07 Déc 2008, 14:49

A(x)=x*racine(1-x^2)
...

/ montrer que le triangle AMM' d'aire maximale est équilatéral.

Racine de la dérivée
...

par **Swann** » 07 Déc 2008, 15:59

mais c'est pour la deuxieme question ça non ??

pour trouver l'aire en fonction de x, c'est : AH x HM ( je m'étais trompée de formule :s)

mais comment faire pour transformer ça en fonction de x.... ?

par **Mathusalem** » 07 Déc 2008, 16:09

Swann a écrit:mais c'est pour la deuxieme question ça non ??

pour trouver l'aire en fonction de x, c'est : AH x HM ( je m'étais trompée de formule :s)

mais comment faire pour transformer ça en fonction de x.... ?

La hauteur du triangle est [A-x].
ensuite, il faut trouver sa base. Si tu connais l'équation d'un cercle centré en l'origine, tu peux, pour un certain x, trouver la valeur y ( en changeant l'équation

pour la mettre sous forme y = .. )

2y = la base, tu as donc [A-x]*2y/2 = [A-x]*y = A(x)
Tu as, grâce à l'équation du cercle, la possibilité d'exprimer y en fonction de x, est là, t'es champion

A+

par **Swann** » 07 Déc 2008, 16:27

pour cela il faut bien prendre le point H comme origine de repere
...enfin.. h de coordonnées (0,0) et comme ça je trouve y=1
c'est ça ??
mais .. je peux pas transformer le A ( pour exprimer la hauteur) en un nombre

il est existe pas une formule pour passer de [AH] à une écriture en fonction de x si j'ai les coordonnée des deux points ??

par **Mathusalem** » 07 Déc 2008, 16:40

Aie aie aie... Pourquoi recourir aux formules ? Faisons plutôt appel à notre intelligence innée, n'allons-nous pas.

Le point h, tu peux le mettre ou tu veux entre les deux extrêmités A' A du cercle. N'est-ce pas ? Maintenant, tu cherches le triangle AMM'
Quel que soit l'endroit entre A et A' où tu places h, la hauteur du triangle sera la distance entre A et h, n'est-ce pas ?
Par conséquent, la hauteur du triangle est [A-h]
Et on te dit quoi ? nommer h comme la variable x ! Vu que h est variable, on l'appelle x. Tu as donc [A-x] comme hauteur pour ton triangle. Mais que vaut A ? A est l'intersection du cercle de rayon 1 et de l'axe Ox ! Réfléchis, et réfléchis fort.

Ensuite, tu veux trouver la base du triangle selon où tu places ton h (donc ton x).

Si tu as fait un dessin, tu te rends compte que la base du triangle est égale à deux fois la distance hm ou hm'

Cette distance correspond à l'ordonnée de la fonction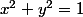

Donc

y =

Tu as ta fonction. y est l'ordonnée, tu as donc 2y = la base exprimée selon x.

Tu devrais t'en sortir grassement

par **Swann** » 07 Déc 2008, 16:49

alors...j'ai réfléchis !

et d'apres moi.. A vaut 1... donc on a la hauteur AH égale a (1-x)

et la base égale a 2y=2racine de (1-x²)

mais pour trouver A(x) j'ai pas besoin de passer par 2y, y nous suffit non ?

l'aire n'est donc pas égale à HMxAH ??? ce qui ferait : A(x)=(x-1)racine de (1-x²)
....

par **Mathusalem** » 07 Déc 2008, 16:51

Swann a écrit:alors...j'ai réfléchis !

et d'apres moi.. A vaut 1... donc on a la hauteur AH égale a (1-x)

et la base égale a 2y=2racine de (1-x²)

mais pour trouver A(x) j'ai pas besoin de passer par 2y, y nous suffit non ?

l'aire n'est donc pas égale à HMxAH ??? ce qui ferait : A(x)=(x-1)racine de (1-x²)
....

Aire triangle = Base * hauteur / 2
[1-x]*2y/2

Donc tu as ta réponse

Et vérifie ce qui est en rouge !

par **Swann** » 07 Déc 2008, 17:07

ouii c'était (1-x) et non (x-1)

j'ai donc trouvé A(x)=(1-x) racine de (1-x²)

:D

merciiii beaucoup !!!!

par **phryte** » 07 Déc 2008, 17:09

Plutôt :
A(x)=x*racine(1-x^2)

par **Swann** » 07 Déc 2008, 17:50

hein ???? pourquoi ...?

par **Mathusalem** » 07 Déc 2008, 19:25

Swann a écrit:hein ???? pourquoi ...?

je me demande aussi pourquoi. Dans le triangle AMM', la hauteur est [A-X]

par **Swann** » 07 Déc 2008, 19:35

ahhh ça me rassure !
donc ce que j'ai trouvé c'est juste ??

en plus je pense que oui, car il y avait des questions au dessus de cette question la, en rapport avec une fonction telle que f(x)=(1-x) racine de (1-x²)

donc ça me semblerait logique !!!

mais j'essaie de prouver que l'aire maximale serait pour un triangle equilaterale.. mais je sais pas comment démarrer :s

par **Mathusalem** » 07 Déc 2008, 21:49

Tu as vu les dérivées ?

PS: Oui, ce que tu as trouvé est juste.

par **Swann** » 07 Déc 2008, 21:56

oui oui j'ai vu les dérivées !

par **Swann** » 07 Déc 2008, 21:56

je dois m'en servir pour le triangle equilatéral ?

par **Mathusalem** » 08 Déc 2008, 00:45

Oui. Tu as la fonction de l'aire selon x. Cherche pour quel x est-ce que A(x) est maximal. Ça te donnera le x pour lequel la valeur de l'aire A(x) est maximale. Après, en regardant la valeur de x et quelques considérations géométriques, tu devrais pouvoir conclure qu'il s'agit d'un triangle equilatéral.

A+

par **phryte** » 08 Déc 2008, 07:56

Bonjour.
Vous avez raison j'ai étudié le triangle OMM' !

Aire A(x) d'un triangle

Aire A(x) d'un triangle

Qui est en ligne