Continuité et compacité

par **Maxke** » 06 Déc 2008, 17:19

Bonjour,

Je dois rendre un travail mardi. Seulement voilà, je ne comprends même pas l'énoncé ! Je suis étudiant en 1e à l'unif, en maths. Je vous retranscris les énoncés:

1er énoncé:

"Rappelons qu'une fonction f est uniformément continue si pour tout £>0 il existe un µ>0 tq:

|x - y| < µ => |f(x)-f(y)| < £ pour tout x,y

Prouver que la fonction f:f(x)=x² est continue, mais n'est pas uniformément continue."

Ici je ne saisis vraiment pas la nuance, je suis perdu...

2e énoncé:

"soit f: R^n -> R^m une fonction continue. Soit K un sous ensemble compact de R^n. montrer (en utilisant la caractérisation d'une fonction continue en termes d'ouverts) que l'image de K par f, f(K), est compacte."

Seulement, voila, je ne trouve pas la notion de compacité dans mon cours, et les énoncés étant rédigés par d'autres profs, je ne vois pas à quoi fait référence la "caractérisation d'une fonction continue en termes d'ouverts".

En vous remerciant d'avance pour votre aide...

par **Antho07** » 06 Déc 2008, 17:34

Pour le premier:
Quelle est la définition d'une fonction continue?
Quelle est la definition d'une fonction uniformement continue?

Quelle différence y a t-il?

Pour le deuxieme:

Une fonction f de R^n dans R^m
est continue si et seulement si pour tout ouvert U de R^m,

est un ouvert de R^n.

Un ensemble K dans R^n est compact si pour tout recouvrement de K par les ouverts de R^n.Il existe un sous recouvrement fini .

Autrement dit , pour famille

d'ouvert de R^n tels que

il existe un sous ensemble J finie de I (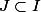

) tels que

On commence donc par prendre un recouvrement de f(K) par des ouverts de R^m.

il faut montrer que il existe un sous-recouvrement fini.
Il pourra être utile de considerer

par **Maxke** » 06 Déc 2008, 17:50

Je te remercie mille fois. Seulement, pour la première question, c'est ce que j'avais fait... Et je n'arrive à rien: si j'ai bien compris il faut arriver à prouver qu'il n'existe pas de relation entre £ et µ qui garantisse l'implication indépendamment de x, mais vraiment ça ne marche pas!

par **ThSQ** » 06 Déc 2008, 17:54

Maxke a écrit:Prouver que la fonction f:f(x)=x² est continue, mais n'est pas uniformément continue."

Sur IR, I presume ....

trouve une suite telle que u(n+1)-u(n) -> 0 mais pas f(u(n+1))-f(u(n)) par exemple.

Le deuxième point est trivial avec la déf de la compacité avec les recouvrements d'ouverts : tu recouvres f(K) avec les ouverts tu en prends les images inverses (qui sont des ouverts), tu extrais un recouv. fini et tu repars de l'autre côté.

par **Maxke** » 06 Déc 2008, 18:19

Je te remercie encore et encore :) Tout cela m'aide beaucoup. Je vais encore te demander conseil sur un point, car je me suis attelé au deuxième, et je suis bloqué à une étape (voici mon ébauche de réponse):

.... comment écrire en maths sur ce forum? Je ne trouve pas dans FAQ...

par **ffpower** » 06 Déc 2008, 18:21

ThSQ a écrit:Sur IR, I presume ....

trouve une suite telle que u(n+1)-u(n) -> 0 mais pas f(u(n+1)-u(n)) par exemple.

ce serait plutot f(u(n+1))-f(u(n)) :we:

Continuité et compacité

Continuité et compacité

Qui est en ligne