Partie entiere
14 messages
- Page 1 sur 1
partie entiere
je voudrais connaitre une formule mathematiques pour calculer la partie entiere ou decimale d un reel(cela revient au meme).
quelqu un peut il m en donner une?????
merci
quelqu un peut il m en donner une?????
merci
partie entiere
je n ai pas compris: |a| est ce la valeur absolue de a ?
de plus je voudrais une formule mathematiques pour tous les cas ici il y a 3 cas a=0, b=0 et sinon
merci quand meme pour la reponse
de plus je voudrais une formule mathematiques pour tous les cas ici il y a 3 cas a=0, b=0 et sinon
merci quand meme pour la reponse
source
pourriez vous me citer la source d'ou vient les formules.
(j'aimerez bien voir la demonstration)
n'avez vous rien de plus simple?
merci d'avance
(j'aimerez bien voir la demonstration)
n'avez vous rien de plus simple?
merci d'avance
alphabetagamma a écrit:pourriez vous me citer la source d'ou vient les formules.
(j'aimerez bien voir la demonstration)
n'avez vous rien de plus simple?
merci d'avance
Ramanujan, c'était un mathématicien indien de génie. Il a pondu des milliers de formules de ce genre, si ça t'intéresses, tu peux te procurer ses "Carnets".
Bah j'ai pas de source, je les ai inventées hier.
J'peux faire la démo de la première c'est pas compliqué.
E(x) =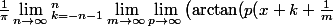)\right))
On commence par regarder, pour y dans R, = \lim_{p \to \infty} \arctan(p y)) .
.
Si y 0, py tend vers +l'infini, et donc f1(y) = +pi/2.
Ensuite on regarde, pour y dans R, = \lim_{m \to \infty} f_1(y+\frac{1}{m}))) .
.
Ça, ça a pour effet de retirer le cas "y=0" dans f1 et de gagner automatiquement la continuité à droite.
Si y =0, ben y+1/m est toujours > 0 donc la suite est constante à +pi/2 donc f2(y) = +pi/2.
Ensuite on regarde, pour y dans R, = \lim_{n \to \infty} \bigsum_{k=-n-1}^n f_2(y+k)) .
.
C'est une fonction en escalier, qui vaut pi*E(y)
Pour tout y, la suite finit par être stationnaire. Si k >= |y|, f2(y+k) vaudra toujours +pi/2 et f2(y-k-1) vaudra toujours -pi/2, donc ils se compensent.
La suite est stationnaire sur un multiple de pi (y'a toujours un nombre pair de termes f2(y+k), qui sont +ou - pi/2).
La fonction est continue à droite.
Ses discontinuités sont à chaque entier, quand on passe de la gauche à la droite d'un entier, y'a un f2 dans la somme qui passe de -pi/2 à +pi/2 donc la différence est exactement de pi.
f3(0) = 0 parceque pour tout k, f2(0+k) + f2(0-k-1) = +pi/2 -pi/2 = 0.
Donc il reste juste à diviser par pi pour avoir la fonction partie entière.
J'peux faire la démo de la première c'est pas compliqué.
E(x) =
On commence par regarder, pour y dans R,
Si y 0, py tend vers +l'infini, et donc f1(y) = +pi/2.
Ensuite on regarde, pour y dans R,
Ça, ça a pour effet de retirer le cas "y=0" dans f1 et de gagner automatiquement la continuité à droite.
Si y =0, ben y+1/m est toujours > 0 donc la suite est constante à +pi/2 donc f2(y) = +pi/2.
Ensuite on regarde, pour y dans R,
C'est une fonction en escalier, qui vaut pi*E(y)
Pour tout y, la suite finit par être stationnaire. Si k >= |y|, f2(y+k) vaudra toujours +pi/2 et f2(y-k-1) vaudra toujours -pi/2, donc ils se compensent.
La suite est stationnaire sur un multiple de pi (y'a toujours un nombre pair de termes f2(y+k), qui sont +ou - pi/2).
La fonction est continue à droite.
Ses discontinuités sont à chaque entier, quand on passe de la gauche à la droite d'un entier, y'a un f2 dans la somme qui passe de -pi/2 à +pi/2 donc la différence est exactement de pi.
f3(0) = 0 parceque pour tout k, f2(0+k) + f2(0-k-1) = +pi/2 -pi/2 = 0.
Donc il reste juste à diviser par pi pour avoir la fonction partie entière.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
