Bonjour
J'aimerais montrer que les images par un homéomorphisme de 2 cercles entrelacés sont toujours entrelacées. Le problème est que je ne connais pas du tout les outils de la théorie des noeuds...
Est-il possible de m'en sortir qu'avec des considèration topologiques basiques? Le fait est que je travail dans R³, qui est un espace avec lequel il est facile de travailler... Mais je ne vois pas comment exprimer cette propriété d'etre entrelacés, et donc je ne vois pas comment montrer qu'un homéomorphisme la preserve...
Entrelacs de cercles dans R³
7 messages
- Page 1 sur 1
Bonjour,
Je vais essayer de faire avancer un peu le truc, mais je suis pas super sur de moi. Je me rappelle plus exactement comment on definit ce fait d'etre enlace mais essayons : tu oriente C1 et C2. Prend ton cercle C1. Dans R3 tu peux le reboucher en un disque, que tu oriente avec C1. Maintenant, ton disque tu peux le prendre de facon que son intersection avec C2 soit transverse. A ce moment la tu compte le nombre de points d'intersections avec signe donne par les orientations. Tu fais la somme de tout ca et ca m'a l'air de bien mesurer le nombre de fois que C2 tourne autour de C1. De plus ca ne depend pas du disque choisi (je te laisse le verifier :zen: ).
Ensuite ton homeo il va t'envoyer tes cercles sur des cercles et ton disque sur un disque. Bon par contre il ya le probleme de l'orientation, mais ca doit pas etre trop grave. J'ai envie de dire que tu obtient a la fin + ou - le nombre d'entrelacement que tu avait avant d'appliquer ton homeo.
Ok ben c'est pas super simple et pas super clair, mais pour l'instant j'ai pas vraiment d'idee plus simple.
Je vais essayer de faire avancer un peu le truc, mais je suis pas super sur de moi. Je me rappelle plus exactement comment on definit ce fait d'etre enlace mais essayons : tu oriente C1 et C2. Prend ton cercle C1. Dans R3 tu peux le reboucher en un disque, que tu oriente avec C1. Maintenant, ton disque tu peux le prendre de facon que son intersection avec C2 soit transverse. A ce moment la tu compte le nombre de points d'intersections avec signe donne par les orientations. Tu fais la somme de tout ca et ca m'a l'air de bien mesurer le nombre de fois que C2 tourne autour de C1. De plus ca ne depend pas du disque choisi (je te laisse le verifier :zen: ).
Ensuite ton homeo il va t'envoyer tes cercles sur des cercles et ton disque sur un disque. Bon par contre il ya le probleme de l'orientation, mais ca doit pas etre trop grave. J'ai envie de dire que tu obtient a la fin + ou - le nombre d'entrelacement que tu avait avant d'appliquer ton homeo.
Ok ben c'est pas super simple et pas super clair, mais pour l'instant j'ai pas vraiment d'idee plus simple.
Bonjour,
sans vouloir écrire trop de bêtises, il me semble qu'en joignant un arc
d'un cercle à l'autre, on obtient une courbe qui a un groupe d'homotopie
de lacets (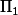 ) isomorphe à un groupe libre engendré par deux éléments
) isomorphe à un groupe libre engendré par deux éléments  et
et  , un truc qui ressemble à ce que l'on obtient quand on concatène sans commutativité des mots composés de lettres
, un truc qui ressemble à ce que l'on obtient quand on concatène sans commutativité des mots composés de lettres  .
.
et qu'un homéomorphisme qui les désentrelace,
induirait un isomorphisme de groupe sur commutatif,ce qui n'est pas possible.
commutatif,ce qui n'est pas possible.
sans vouloir écrire trop de bêtises, il me semble qu'en joignant un arc
d'un cercle à l'autre, on obtient une courbe qui a un groupe d'homotopie
de lacets (
et qu'un homéomorphisme qui les désentrelace,
induirait un isomorphisme de groupe sur
Hum je crois que zenaf et mathelot on mal compris ce que je voulais dire par entrelacés. Je ne considère pas la wedge (orth?) de 2 cercles, mais 2 cercles qui se passe mutuellement à l'intérieure. Donc un truc comme ca:
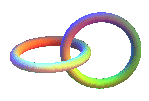
Ensuite R.C. j'ai pas vraiment compris ton explications :/ Mais le cas que je traite me semble plus simple, étant donné que chaque cercle ne tourne qu'une seule fois autours de l'autre...
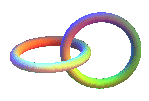
Ensuite R.C. j'ai pas vraiment compris ton explications :/ Mais le cas que je traite me semble plus simple, étant donné que chaque cercle ne tourne qu'une seule fois autours de l'autre...
Ah ok, si tu veux juste regarder le cas qui est sur la figure, et bien tu rebouche un des deux cercles en un disque. tu vois que l'intersection de ce disque avec l'autre cercle c'est un point, donc quand tu regarde l'image par l'homeo, tu as deux cercles, dont l'un est bouche en un disque, et l'autre intersecte ce disque en exactement un point. Maintenant , je pense que si tu as deux cercles dans cette configuration, ils sont entrelaces.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
