Bonjour
A est une matrice à coeff réels vérifiant A^p=I.
Il faut montrer que son spectre est égal aux racine p-ièmes de l'unité.
J'arrive à mq une inclusion avec les racines du polynome annulateur.
Comment mq l'autre inclusion i.e que les racines p iemes sont incluses dans le spectre ?
Merci
A^p=I
3 messages
- Page 1 sur 1
Salut,
Le truc c'est que tu n'as pas précisé p. Est-ce le plus petit p possible?
et parler "du polynôme annulateur" ne veut rien dire: l'ensemble des polynômes annulateurs de A est un idéal, de la forme , ie engendré par le polynôme minimal de A
, ie engendré par le polynôme minimal de A 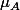 .
.
Cordialement,
Luc
zobobo a écrit:Bonjour
A est une matrice à coeff réels vérifiant A^p=I.
Il faut montrer que son spectre est égal aux racine p-ièmes de l'unité.
J'arrive à mq une inclusion avec les racines du polynome annulateur.
Comment mq l'autre inclusion i.e que les racines p iemes sont incluses dans le spectre ?
Merci
Le truc c'est que tu n'as pas précisé p. Est-ce le plus petit p possible?
et parler "du polynôme annulateur" ne veut rien dire: l'ensemble des polynômes annulateurs de A est un idéal, de la forme
Cordialement,
Luc
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
