Equation de récurence
23 messages
- Page 1 sur 2 - 1, 2
equation de récurence
Bonjour a toutes et a tous !
Voila mon petit probleme, j'ai l'équation de recurence suivante :
T(1)=1
T(n)=3T(n/2) + n²
Je cherche a trouver l'ordre de grandeur asymptotique de T(n), et j'avou que je bloque pas mal ... Si quelqu'un pouvait venir a mon secours, ça serait vraiment gentil !
Merci d'avance
Voila mon petit probleme, j'ai l'équation de recurence suivante :
T(1)=1
T(n)=3T(n/2) + n²
Je cherche a trouver l'ordre de grandeur asymptotique de T(n), et j'avou que je bloque pas mal ... Si quelqu'un pouvait venir a mon secours, ça serait vraiment gentil !
Merci d'avance
Salut,
Les informaticiens se sortent souvent de cette remarque en disant que T est croissante (c'est une complexité) et qu'il suffit donc de le calculer pour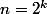 . On en pense ce qu'on veut ...
. On en pense ce qu'on veut ...
Tu obtiens une récurrence du type , ça doit se résoudre, mais à vue de nez u_n est de l'ordre de 4^n, ce qui ferait T(n) de l'ordre de n^2. (Je peux me tromper)
, ça doit se résoudre, mais à vue de nez u_n est de l'ordre de 4^n, ce qui ferait T(n) de l'ordre de n^2. (Je peux me tromper)
Luc
Les informaticiens se sortent souvent de cette remarque en disant que T est croissante (c'est une complexité) et qu'il suffit donc de le calculer pour
Tu obtiens une récurrence du type
Luc
ok merci beaucoup de m'aider !
donc si on considere que Un est de l'ordre de 4^n, donc T(n) est de l'ordre de n².
Si je pose Uk=T(2^k), comment je peut montrer que Uk vérifie la récurrence
Uk - 7U(k-1) + 12U(k-2) pour k>=2
Et comment la résoudre ? vous avez une piste pour m'aider ?
merci d'avance
Cordialement
donc si on considere que Un est de l'ordre de 4^n, donc T(n) est de l'ordre de n².
Si je pose Uk=T(2^k), comment je peut montrer que Uk vérifie la récurrence
Uk - 7U(k-1) + 12U(k-2) pour k>=2
Et comment la résoudre ? vous avez une piste pour m'aider ?
merci d'avance
Cordialement
thotoss a écrit:ok merci beaucoup de m'aider !
donc si on considere que Un est de l'ordre de 4^n, donc T(n) est de l'ordre de n².
Si je pose Uk=T(2^k), comment je peut montrer que Uk vérifie la récurrence
Uk - 7U(k-1) + 12U(k-2) pour k>=2
Et comment la résoudre ? vous avez une piste pour m'aider ?
merci d'avance
Cordialement
Je ne comprends pas ta question.
Tu veux montrer que Uk - 7U(k-1) + 12U(k-2) = quelque chose?
Luc
ah ok merci beaucoup j'avais pas bien compris en fait merci bien !
donc ça c'est T(n) en fonction de n lorsque n=2^k
Je voudrais aussi trouver l'odre de grandeur asymptotique de T(n) sans passer par n=2^k, juste avec l'equation de recurrence de mon premier post ... commetn je peux faire alors ? parsque c'est la aussi que je me mélange ..
merci beaucoup de m'aider je galere un peu la ...
donc ça c'est T(n) en fonction de n lorsque n=2^k
Je voudrais aussi trouver l'odre de grandeur asymptotique de T(n) sans passer par n=2^k, juste avec l'equation de recurrence de mon premier post ... commetn je peux faire alors ? parsque c'est la aussi que je me mélange ..
merci beaucoup de m'aider je galere un peu la ...
re bonjour !
alors voila clairement ce que je cherche maintenant :
j'ai toujous mon equation de recurence suivante (1) :
T(1)=1
T(n)=3T(n/2)+n²
et je voudrais juste trouver l'ordre de grandeur asymptotique de T(n), sans utiliser n=2^k, parcque ça m'est demandé que aprés ... comment je peux faire ?
merci beaucoup de m'aider !
cdt
alors voila clairement ce que je cherche maintenant :
j'ai toujous mon equation de recurence suivante (1) :
T(1)=1
T(n)=3T(n/2)+n²
et je voudrais juste trouver l'ordre de grandeur asymptotique de T(n), sans utiliser n=2^k, parcque ça m'est demandé que aprés ... comment je peux faire ?
merci beaucoup de m'aider !
cdt
Comment ça c'est quoi ? je ne sais pas en fait ... mon énoncé n'est pas trés claire : voila precisement ce qu'il dit :
Soit l'equation de récurence (1) :
T(1)=1
T(n)=3T(n/2)+n²
Trouvez l'ordre de grandeur asymptotique de T(n).
Et je vois pas comment faire ... surtout que le suite de l'exo est encore plus incomprehensible .... :triste:
Soit l'equation de récurence (1) :
T(1)=1
T(n)=3T(n/2)+n²
Trouvez l'ordre de grandeur asymptotique de T(n).
Et je vois pas comment faire ... surtout que le suite de l'exo est encore plus incomprehensible .... :triste:
ok donc j'ai reussi a montrer que l'ordre de grandeur de T(n) est n2 . Mais maintenant je bloque sur cette question :
On pose Uk=T(2^k) . Montrez que Uk vérifie la récurence (2) :
Uk - 7U(k-1) + 12U(k-2) pour k>=2
et reolvez l'equation.
Mais je ne trouve pas que c'est une équation !! enfin c'est egale a rien quoi ... je comprend pas ... merci si vous pouvez m'aider !!
cdt
On pose Uk=T(2^k) . Montrez que Uk vérifie la récurence (2) :
Uk - 7U(k-1) + 12U(k-2) pour k>=2
et reolvez l'equation.
Mais je ne trouve pas que c'est une équation !! enfin c'est egale a rien quoi ... je comprend pas ... merci si vous pouvez m'aider !!
cdt
black a écrit:ok donc j'ai reussi a montrer que l'ordre de grandeur de T(n) est n2 . Mais maintenant je bloque sur cette question :
On pose Uk=T(2^k) . Montrez que Uk vérifie la récurence (2) :
Uk - 7U(k-1) + 12U(k-2) pour k>=2
et reolvez l'equation.
Mais je ne trouve pas que c'est une équation !! enfin c'est egale a rien quoi ... je comprend pas ... merci si vous pouvez m'aider !!
cdt
Bonsoir,
Je ne comprends pas pourquoi tu reviens à cette question. yos t'a déja donné la réponse. Le
L'équation est vraisemblablement
Je me demandais un truc: dans quel contexte est posé ton exercice? C'est des maths ou de l'info?
Et question subsidiaire: quelle est la suite de l'exo?
Merci,
Luc
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
